
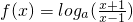 ,(其中a>0且a≠1).
,(其中a>0且a≠1). 得x<-1或x>1,即f(x)的定义域为{x|x<-1或x>1},
得x<-1或x>1,即f(x)的定义域为{x|x<-1或x>1},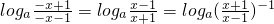 =-f(x)
=-f(x)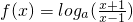 由y=logat和
由y=logat和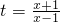 复合而成,
复合而成, 在(-∞,-1)和(1,+∞)上都为减函数,
在(-∞,-1)和(1,+∞)上都为减函数,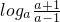 =1,即a2-2a-1=0,
=1,即a2-2a-1=0, ,又因为a>1,故a=
,又因为a>1,故a=
 与
与 互为导数,其对数值互为相反数.
互为导数,其对数值互为相反数.

科目:高中数学 来源: 题型:
(06年辽宁卷理)(12分)
已知函数f(x)=![]() ,其中a , b , c是以d为公差的等差数列,,且a>0,d>0.设
,其中a , b , c是以d为公差的等差数列,,且a>0,d>0.设![]() [1-
[1-![]() ]上,
]上,![]() ,在
,在![]() ,将点
,将点![]() A, B, C
A, B, C
(I)求![]()
(II)若ABC有一边平行于x轴,且面积为![]() ,求a ,d的值
,求a ,d的值
查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江省哈尔滨六中高二(下)期中数学试卷(文科)(解析版) 题型:解答题
 .,其中a,b∈R
.,其中a,b∈R查看答案和解析>>
科目:高中数学 来源:2015届新课标高一下学期第四次月考数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函数 ,
, (其中A>0,
(其中A>0, >0,
>0, <
<
 的部分图象如图所示,求这个函数的解析式.
的部分图象如图所示,求这个函数的解析式.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省5月第一次周考理科数学试卷(解析版) 题型:解答题
已知函数 满足
满足 ,其中a>0,a≠1.
,其中a>0,a≠1.
(1)对于函数 ,当x∈(-1,1)时,f(1-m)+f(1-m2)<0,求实数m的取值集合;
,当x∈(-1,1)时,f(1-m)+f(1-m2)<0,求实数m的取值集合;
(2)当x∈(-∞,2)时,
 的值为负数,求
的值为负数,求 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2010年北京市丰台区高三第二次模拟考试数学(理) 题型:解答题
(12分)已知函数f(x)= (其中A>0,
(其中A>0, )的图象如图所示。
)的图象如图所示。

(Ⅰ)求A,w及j的值;
(Ⅱ)若tana=2, ,求 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com