解:(1)任取x
1,x
2∈R,且x
1<x
2,
则F(x
1)-F(x
2)
=f(x
1)-f(a-x
1)-[f(x
2)-f(a-x
2)].
=[f(x
1)-f(x
2)]+[f(a-x
2)-f(a-x
1)].
∵x
1<x
2,∴-x
1>-x
2,∴a-x
1>a-x
2,
∵函数f(x)是定义在R上的增函数,∴f(x
1)<f(x
2),f(a-x
2)<f(a-x
1).
∴f(x
1)-f(x
2)<0,f(a-x
2)-f(a-x
1)<0.
∴[f(x
1)-f(x
2)]+[f(a-x
2)-f(a-x
1)]<0.
即F(x
1)<F(x
2),
∴F(x)是R上的增函数.
(2)设M(x
0,y
0)为函数y=F(x)的图象上任一点,设点M(x
0,y
0)关于点(

,0)的对称点为N(m,n),
则

=
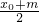
,0=
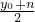
,,∴m=a-x
0,n=-y
0,
∵把m=a-x
0代入F(x)=f(x)-f(a-x).
得,f(a-x
0)-f(a-a+x
0)=f(a-x
0)-f(x
0)=-y
0=n
即点N(m,n)在函数F(x)的图象上.
∴函数y=F(x)的图象关于点(

,0)成中心对称图形.
分析:(1)利用函数单调性的定义证明函数的单调性的步骤,第一步,设所给区间上任意两个自变量x
1,x
2,且x
1<x
2,第二步,作差比较F(x
1)与F(x
2)的大小,第三步,得出结论,本题严格按照步骤去做,比较F(x
1)与F(x
2)时,要借助函数f(x)的单调性.
(2)要证明函数y=F(x)的图象关于点(

,0)成中心对称图形,只需证明函数y=F(x)的图象上任意一点关于点
(

,0)的对称点在函数y=F(x)的图象上即可,先利用中点坐标公式求出函数y=F(x)的图象上任意一点关于点
(

,0)的对称点坐标,再代入函数y=F(x)的解析式,看是否成立即可.
点评:本题主要考查定义法证明函数的单调性,以及抽象函数对称性的判断,做题时严格按照定义去做.

 ,0)成中心对称图形.
,0)成中心对称图形. ,0)的对称点为N(m,n),
,0)的对称点为N(m,n), =
=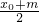 ,0=
,0=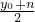 ,,∴m=a-x0,n=-y0,
,,∴m=a-x0,n=-y0, ,0)成中心对称图形.
,0)成中心对称图形. ,0)成中心对称图形,只需证明函数y=F(x)的图象上任意一点关于点
,0)成中心对称图形,只需证明函数y=F(x)的图象上任意一点关于点 ,0)的对称点在函数y=F(x)的图象上即可,先利用中点坐标公式求出函数y=F(x)的图象上任意一点关于点
,0)的对称点在函数y=F(x)的图象上即可,先利用中点坐标公式求出函数y=F(x)的图象上任意一点关于点 ,0)的对称点坐标,再代入函数y=F(x)的解析式,看是否成立即可.
,0)的对称点坐标,再代入函数y=F(x)的解析式,看是否成立即可.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案 已知函数f(x)=x+
已知函数f(x)=x+