
【题目】若数列{an}的前n项和Sn满足Sn=2an+n.
(Ⅰ)求证:数列{an﹣1}是等比数列;
(Ⅱ)记bn=![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品.为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如下表所示:
,如下表所示:

已知![]() .
.
(1)求出![]() 的值;
的值;
(2)已知变量![]() ,
, ![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(3)用![]() 表示用正确的线性回归方程得到的与
表示用正确的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 的残差的绝对值
的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有1个是“好数据”的概率.
称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有1个是“好数据”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC三个顶点坐标分别为:A(1,0),B(1,4),C(3,2),直线l经过点(0,4).
(1)求△ABC外接圆⊙M的方程;
(2)若直线l与⊙M相交于P,Q两点,且|PQ|=2 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
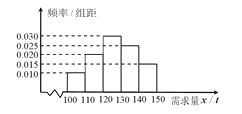
【题目】经销商经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润500元,未售出的产品,每
该产品获利润500元,未售出的产品,每![]() 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (
(![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, ![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)根据直方图估计利润![]() 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足:a1=1,an+1=3an , n∈N+ .
(1)求{an}的通项公式及前n项和Sn;
(2)已知{bn}是等差数列,Tn为前n项和,且b1=a2 , b3=a1+a2+a3 , 求T20 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于95为正品,小于95为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
机床甲 | 8 | 12 | 40 | 32 | 8 |
机床乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为正品的概率;
(2)甲机床生产一件零件,若是正品可盈利160元,次品则亏损20元;乙机床生产一件零件,若是正品可盈利200元,次品则亏损40元,在(1)的前提下,现需生产这种零件2件,以获得利润的期望值为决策依据,应该如何安排生产最佳?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为对考生的月考成绩进行分析,某地区随机抽查了![]() 名考生的成绩,根据所得数据画了如下的样本频率分布直方图.
名考生的成绩,根据所得数据画了如下的样本频率分布直方图.
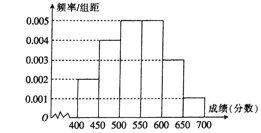
(1)求成绩在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析成绩与班级、学校等方面的关系,必须按成绩再从这![]() 人中用分层抽样方法抽取出
人中用分层抽样方法抽取出![]() 人作出进一步分析,则成绩在
人作出进一步分析,则成绩在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asin B=![]() b.
b.
(1)求角A的大小; (2)若a=6,b+c=8,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017 年省内某事业单位面向社会公开招骋工作人员,为保证公平竞争,报名者需要参加笔试和面试两部分,且要求笔试成绩必须大于或等于![]() 分的才有资格参加面试,
分的才有资格参加面试, ![]() 分以下(不含
分以下(不含![]() 分)则被淘汰,现有
分)则被淘汰,现有![]() 名竞骋者参加笔试,参加笔试的成绩按区间
名竞骋者参加笔试,参加笔试的成绩按区间![]() 分段,其频率分布直方图如图所示(频率分布直方图有污损),但是知道参加面试的人数为
分段,其频率分布直方图如图所示(频率分布直方图有污损),但是知道参加面试的人数为![]() ,且笔试成绩在
,且笔试成绩在![]() 的人数为
的人数为![]() .
.

(1)根据频率分布直方图,估算竞骋者参加笔试的平均成绩;
(2)若在面试过程中每人最多有![]() 次选题答题的机会,累计答对
次选题答题的机会,累计答对![]() 题或答错
题或答错![]() 题, 答对
题, 答对![]() 题者方可参加复赛,已知面试者甲答对每一个问题的概率都相同,并且相互之间没有影响,若他连续三次答题中答对一次的概率为
题者方可参加复赛,已知面试者甲答对每一个问题的概率都相同,并且相互之间没有影响,若他连续三次答题中答对一次的概率为![]() ,求面试者甲答题个数
,求面试者甲答题个数![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com