练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．电影院一排10个位置，甲、乙、丙三人去看电影，要求他们坐在同一排，那么他们每人左右两边都有空位且甲坐在中间的坐法有40种．

    分析 根据题意，先排好7个空座位，注意空座位是相同的，其中有6个空位符合条件，考虑顺序，将3人插入6个空位中，注意甲必须在三人中间，由倍分法分析可得答案．

    解答 解：先排7个空座位，由于空座位是相同的，则只有1种情况，其中有6个空位符合条件，
    考虑三人的顺序，将3人插入6个空位中，则共有1×A63=120种情况，
    由于甲必须坐在三人中间，则有符合要求的坐法有$\frac{1}{3}$×120=40种；
    故答案为：40．

    点评 本题考查排列、组合的应用，对于不相邻的问题采用插空法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

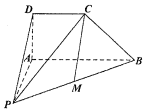    13．如图，在四棱锥P-ABCD中，CD∥AB，AD=DC=$\frac{1}{2}$AB．
    （1）若M是PB的中点，求证：CM∥平面PAD；
    （2）若AD⊥AB，BC⊥PC，求证：平面PAC⊥平面PBC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知正方形ABCD的边长为2，E是BC的中点，以点C为圆心，CE长为半径作圆，点P是该圆上的任一点，则$\overrightarrow{AP}•\overrightarrow{DE}$的取值范围是（　　）
    A．$[0，2+\sqrt{6}]$B．$[2-\sqrt{6}，2+\sqrt{6}]$C．$[0，2+\sqrt{5}]$D．$[2-\sqrt{5}，2+\sqrt{5}]$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

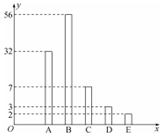    11．某校为缓解高三学生的高考压力，经常举行一些心理素质综合能力训练活动，经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试，并将其成绩分为A、B、C、D、E五个等级，统计数据如图所示（视频率为概率），根据图中抽样调查的数据，回答下列问题：
    （1）试估算该校高三年级学生获得成绩为B的人数；
    （2）若等级A、B、C、D、E分别对应100分、90分、80分、70分、60分，学校要求当学生获得的等级成绩的平均分大于90分时，高三学生的考前心理稳定，整体过关，请问该校高三年级目前学生的考前心理稳定情况是否整体过关？
    （3）以每个学生的心理都培养成为健康状态为目标，学校决定对成绩等级为E的16名学生（其中男生4人，女生12人）进行特殊的一对一帮扶培训，从按分层抽样抽取的4人中任意抽取2名，求恰好抽到1名男生的概率..

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．如图，在棱长为1的正方体ABCD-A1B1C1D1中，P，Q，R分别是棱AB，AD，AA1的中点．以△PQR为底面作一个直三棱柱，使其另一个底面的三个顶点也都在此正方体的表面上．则这个直三棱柱的体积是$\frac{3}{16}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知$\overrightarrow a=（1，1）$，$\overrightarrow b=（1，0）$，则当$|{\overrightarrow a-t\overrightarrow b}|$取最小值时，实数t=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．若圆C与y轴相切于点P（0，1），与x轴的正半轴交于A，B两点，且|AB|=2，则圆C的标准方程是（　　）
    A．${（x+\sqrt{2}）^2}+{（y+1）^2}=2$B．${（x+1）^2}+{（y+\sqrt{2}）^2}=2$C．${（x-\sqrt{2}）^2}+{（y-1）^2}=2$D．${（x-1）^2}+{（y-\sqrt{2}）^2}=2$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．在区间[-4，1]上随机地取一个实数x，若x满足|x|＜a的概率为$\frac{4}{5}$，则实数a的值为（　　）
    A．$\frac{1}{2}$B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知等比数列{an}满足a1=2，a2=4（a3-a4），数列{bn}满足bn=3-2log2an．
    （1）求数列{an}，{bn}的通项公式；
    （2）令cn=$\frac{{b}_{n}}{{a}_{n}}$，求数列{cn}的前n项和Sn；
    （3）若λ＞0，求对所有的正整数n都有2λ2-kλ+2＞a2nbn成立的k的取值范围．

    查看答案和解析>>

    同步练习册答案