
| A. | $[0,2+\sqrt{6}]$ | B. | $[2-\sqrt{6},2+\sqrt{6}]$ | C. | $[0,2+\sqrt{5}]$ | D. | $[2-\sqrt{5},2+\sqrt{5}]$ |
分析 由题意,建立平面直角坐标系,设出各点坐标,利用数量积的坐标运算,得到P的关系式,结合点在圆上得到所求范围.
解答 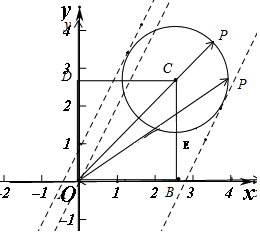 解:由题意,建立平面直角坐标系,如图则A(0,0),C(2,2),D(0,2),E(2,1),P(x,y),则(x-2)2+(y-2)2=1,
解:由题意,建立平面直角坐标系,如图则A(0,0),C(2,2),D(0,2),E(2,1),P(x,y),则(x-2)2+(y-2)2=1,
$\overrightarrow{AP}$=(x,y),$\overrightarrow{DE}$=(2,-1),
所以$\overrightarrow{AP}•\overrightarrow{DE}$=2x-y=z,则y=2x-z,当此直线与圆相切时使得在y轴的截距取得最值,所以$\frac{|2-z|}{\sqrt{5}}=1$,解得z=2$±\sqrt{5}$,
所以$\overrightarrow{AP}•\overrightarrow{DE}$的取值范围是[2-$\sqrt{5}$,2+$\sqrt{5}$];
故选D.
点评 本题考查了向量的坐标运算、点与圆的位置关系,考查了分类讨论思想方法,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [1,2] | C. | (1,3) | D. | (1,$\frac{3}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{6}{2×{3}^{2016}-1}$ | C. | $\frac{2}{2×{3}^{2016}-1}$ | D. | $\frac{2}{2×{3}^{2015}-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一次数学考试后,某老师从自己所带的两个班级中各抽取6人,记录他们的考试成绩,得到如图所示的茎叶图.已知甲班6名同学成绩的平均数为82,乙班6名同学成绩的中位数为77,则x-y=( )
一次数学考试后,某老师从自己所带的两个班级中各抽取6人,记录他们的考试成绩,得到如图所示的茎叶图.已知甲班6名同学成绩的平均数为82,乙班6名同学成绩的中位数为77,则x-y=( )| A. | 3 | B. | -3 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有0条 | B. | 有1条 | C. | 有2条 | D. | 有3条 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<1} | B. | {x|-2≤x≤2} | C. | {x|1<x≤2} | D. | {x|x<2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com