
【题目】已知定义在![]() 上的函数
上的函数![]() 的图像关于直线
的图像关于直线![]() 对称,且当
对称,且当![]() 时,
时,![]() ,过点
,过点![]() 作曲线
作曲线![]() 的两条切线,若这两条切线互相垂直,则该函数
的两条切线,若这两条切线互相垂直,则该函数![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
当![]() 时,
时,![]() ,可得函数
,可得函数![]() 在
在![]() 为增函数,结合函数的对称性可得函数的最小值为
为增函数,结合函数的对称性可得函数的最小值为![]() ,进而分析可得点
,进而分析可得点![]() 作曲线
作曲线![]() 的两条切线的斜率
的两条切线的斜率![]() ,设
,设![]() 右侧的切点为
右侧的切点为![]() ,求出函数的导数,由导数的几何意义可得
,求出函数的导数,由导数的几何意义可得![]() ,即
,即![]() ,结合两点间连线的斜率公式可得
,结合两点间连线的斜率公式可得![]() ,即
,即![]() ,联立两式求出
,联立两式求出![]() 的值,代入函数的解析式可得结果.
的值,代入函数的解析式可得结果.
根据题意,分析可得当![]() 时,
时,![]() ,
,
则函数![]() 在
在![]() 为增函数,
为增函数,
又由函数![]() 的图象关于直线
的图象关于直线![]() 对称,函数
对称,函数![]() 在
在![]() 为减函数,
为减函数,
所以函数的最小值为![]() ,
,
点![]() 作曲线
作曲线![]() 的两条切线,
的两条切线,
则两条切线的关于直线![]() 对称,即两条切线的斜率互为相反数,
对称,即两条切线的斜率互为相反数,
若两条切线互相垂直,切线的斜率![]() ,
,
设![]() 右侧的切点为
右侧的切点为![]() ,
,
因为![]() ,所以导数
,所以导数![]() ,
,
则有![]() ,即
,即![]() ,①
,①
又由切线过点![]() ,可得
,可得![]() ,
,
即![]() ,解可得
,解可得![]() ,②
,②
联立①②可得![]() ,
,
则函数![]() 的最小值为
的最小值为![]() ,故选B.
,故选B.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】已知n为给定的正整数,t为给定的实数,设(t+x)n=a0+a1x+a2x2+…+anxn.
(1)当n=8时.
①若t=1,求a0+a2+a4+a6+a8的值;
②若t=![]() ,求数列{an}中的最大值;
,求数列{an}中的最大值;
(2)若t=![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一湖中有不在同一直线的三个小岛A、B、C,前期为开发旅游资源在A、B、C三岛之间已经建有索道供游客观赏,经测量可知AB两岛之间距离为3公里,BC两岛之间距离为5公里,AC两岛之间距离为7公里,现调查后发现,游客对在同一圆周上三岛A、B、C且位于![]() (优弧)一片的风景更加喜欢,但由于环保、安全等其他原因,没办法尽可能一次游览更大面积的湖面风光,现决定在
(优弧)一片的风景更加喜欢,但由于环保、安全等其他原因,没办法尽可能一次游览更大面积的湖面风光,现决定在![]() 上选择一个点D建立索道供游客游览,经研究论证为使得游览面积最大,只需使得△ADC面积最大即可.则当△ADC面积最大时建立索道AD的长为______公里.(注:索道两端之间的长度视为线段)
上选择一个点D建立索道供游客游览,经研究论证为使得游览面积最大,只需使得△ADC面积最大即可.则当△ADC面积最大时建立索道AD的长为______公里.(注:索道两端之间的长度视为线段)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个正方形花圃被分成5份.
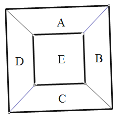
(1)若给这5个部分种植花,要求相邻两部分种植不同颜色的花,己知现有红、黄、蓝、绿4种颜色不同的花,求有多少种不同的种植方法?
(2)若将6个不同的盆栽都摆放入这5个部分,且要求每个部分至少有一个盆栽,问有多少种不同的放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A.若随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]() ;
;
B.已知直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,则“
,则“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
C.若随机变量![]() 服从二项分布:
服从二项分布:![]() ,则
,则![]() ;
;
D.已知直线![]() 经过点
经过点![]() ,则
,则![]() 的取值范围是
的取值范围是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com