
���� ��1����ֱ��l�ļ����귽�̣��æ�cos��-��sin��=1���ɴ������ֱ��l��ֱ�����귽�̣�������C�IJ������������C����ͨ���̣�
��2������C��ʾԲ�ģ�5��0�����뾶r=1��Բ����y=0����A��4��0����B��6��0������A����ֱ��l�ĶԳƵ�A1��A1��1��3������PΪA1B��l�Ľ���ʱ����PAB���ܳ���С���ɴ��������PAB�ܳ�����Сֵ��
��� �⣺��1����ֱ��l�ļ����귽��Ϊ��cos����+$\frac{��}{4}$��=$\frac{\sqrt{2}}{2}$��
����ֱ��l�ļ����귽�̣���$��cos��sin\frac{��}{4}-��sin��cos\frac{��}{4}$=$\frac{\sqrt{2}}{2}$������2�֣�
����cos��-��sin��=1��
��ֱ��l��ֱ�����귽��Ϊx-y=1����x-y-1=0������3�֣�
������C�IJ�������Ϊ$\left\{\begin{array}{l}{x=5+cos��}\\{y=sin��}\end{array}\right.$����Ϊ��������
��������C�IJ������̵�C����ͨ����Ϊ����x-5��2+y2=1������5�֣�
��2���ɣ�1��֪����C��ʾԲ�ģ�5��0�����뾶r=1��Բ��
��y=0����x=4��x=6��
��A������Ϊ��4��0����B������Ϊ��6��0���� ����7�֣�
��A����ֱ��l�ĶԳƵ�A1��A1��1��3��������8�֣�
������֪��PΪA1B��l�Ľ���ʱ����PAB���ܳ���С��
���PAB�ܳ�����СֵΪ��|AP|+|PB|+|AB|=|A1B|+|AB|=$\sqrt{34}+2$������10�֣�
���� ���⿼��ֱ�ߵ�ֱ�����귽�̺����ߵ���ͨ���̵��������������ܳ�����Сֵ�����������ʽ��ֵ�������е��⣬����ʱҪ�������⣬ע�⼫���귽�̡�ֱ�����귽�̡��������̵����ʼ�������ʽ�ĺ������ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
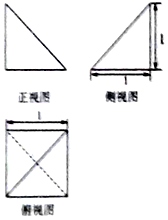
 ��ͼ��������������ֽ�ϣ���ʵ��������ij�����������ͼ���䲿�ֳߴ磬���ö�����Ķ�����ͬһ�����ϣ������ı�������ڣ�������
��ͼ��������������ֽ�ϣ���ʵ��������ij�����������ͼ���䲿�ֳߴ磬���ö�����Ķ�����ͬһ�����ϣ������ı�������ڣ�������| A�� | 8�� | B�� | 18�� | C�� | 24�� | D�� | 8$\sqrt{6}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x��R������x2��1 | B�� | ?x��R��ʹ��x2��1 | ||
| C�� | ?x��R������x��-1��x��1 | D�� | ?x��R��ʹ��x2��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{8}$ | B�� | $\frac{3}{16}$ | C�� | $\frac{��}{8}$ | D�� | $\frac{��}{16}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3�� | B�� | 2�� | C�� | �� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9 | B�� | 10 | C�� | 11 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8�� | B�� | 16�� | C�� | 32�� | D�� | 36�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com