练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．某棱锥的三视图如图所示，则该棱锥的外接球的表面积为（　　）
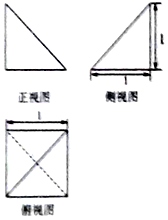
    A．3πB．2πC．πD．4π

    分析 根据三视图知几何体是三棱锥为棱长为1的正方体一部分，并画出直观图，由正方体的性质求出外接球的半径，由球的表面积公式求出该棱锥的外接球的表面积．

    解答 解：根据三视图知几何体是：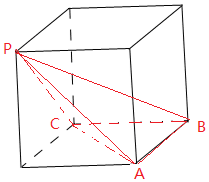
    三棱锥P-ABC为棱长为1的正方体一部分，
    直观图如图所示：
    则三棱锥P-ABC的外接球是此正方体的外接球，
    设外接球的半径是R，
    由正方体的性质可得，2R=$\sqrt{3}$，解得R=$\frac{\sqrt{3}}{2}$，
    所以该棱锥的外接球的表面积S=4πR2=3π，
    故选A．

    点评 本题考查由三视图求几何体外接球的表面积，在三视图与直观图转化过程中，以一个正方体为载体是很好的方式，使得作图更直观，考查空间想象能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．已知某几何体的三视图如图所示，则该几何体的内切球的表面积为（　　）
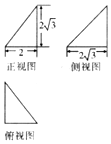
    A．$\frac{2π}{3}$B．$\frac{4π}{3}$C．3πD．4π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．设Sn是等差数列{an}的前n项和，已知S3=6，a4=4．
    （1）求数列{an}的通项公式；
    （2）若bn=3${\;}^{{a}_{n+1}}$-3${\;}^{{a}_{n}}$，求证：$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$＜$\frac{1}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知f（x）=ax2-2（a+1）x+3（a∈R）．
    （1）若函数f（x）在$[{\frac{3}{2}，3}]$单调递减，求实数a的取值范围；
    （2）令h（x）=$\frac{f（x）}{x-1}$，若存在${x_1}，{x_2}∈[{\frac{3}{2}，3}]$，使得|h（x1）-h（x2）|≥$\frac{a+1}{2}$成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．若（x+y）3（2x-y+a）5的展开式中各项系数的和为256，则该展开式中含字母x且x的次数为1的项的系数为0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．在直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos（θ+$\frac{π}{4}$）=$\frac{\sqrt{2}}{2}$，曲线C的参数方程为$\left\{\begin{array}{l}{x=5+cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数）．
    （1）求直线l的直角坐标方程和曲线C的普通方程；
    （2）曲线C交x轴于A、B两点，且点A的横坐标小于点B的横坐标，P为直线l上的动点，求△PAB周长的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．若函数f（x）=$\left\{\begin{array}{l}{\frac{1}{{2}^{x}}-1，x＜1}\\{\frac{lnx}{{x}^{2}}，x≥1}\end{array}\right.$，则函数y=|f（x）|-$\frac{1}{8}$的零点个数为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=|x-2|．
    （1）求不等式f（x）+x2-4＞0的解集；
    （2）设g（x）=-|x+7|+3m，若关于x的不等式f（x）＜g（x）的解集非空，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．某校开展“翻转合作学习法”教学实验，经过一年的实践后，对“翻转班”和“对照班”的全部220名学生的数学学习情况进行测试，按照大于或等于120分为“成绩优秀”，120分以下为“成绩一般”统计，得到如下的2×2列联表．
      成绩优秀 成绩一般 合计
     对照班 20 90 110
     翻转班 40 70 110
     合计 60 160 220
    （Ⅰ）根据上面的列联表判断，能否在犯错误的概率不超过0.001的前提下认为“成绩优秀与翻转合作学习法”有关；
    （Ⅱ）为了交流学习方法，从这次测试数学成绩优秀的学生中，用分层抽样方法抽出6名学生，再从这6名学生中抽3名出来交流学习方法，求至少抽到一名“对照班”学生交流的概率．
    附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$：
     P（K2≥k0） 0.10 0.05 0.025 0.010 0.005 0.001
     k0 2.706 3.841 5.024 6.635 7.879 10.828

    查看答案和解析>>

    同步练习册答案