
分析 (1)对a讨论,a=0,a>0,a<0,结合二次函数的图象和单调性的性质,得到不等式组,解不等式即可得到a的范围;
(2)由题意可得在$x∈[{\frac{3}{2},3}]$上,h(x)max-h(x)min≥$\frac{a+1}{2}$成立,因为$h(x)=\frac{f(x)}{x-1}=a({x-1})+\frac{1-a}{x-1}-2$,令$t=x-1∈[{\frac{1}{2},2}]$,则$g(t)=a•t+\frac{1-a}{t}-2$,$t∈[{\frac{1}{2},2}]$.对a讨论,(i)当a≤0时,(ii)当0<a<1时,求出单调性和最值,即可得到a的范围.
解答 解:(1)①当a=0时,f(x)=-2x+3,显然满足;
②$\left\{\begin{array}{l}a>0\\ \frac{a+1}{a}≥3\end{array}\right.⇒0<a≤\frac{1}{2}$,③$\left\{\begin{array}{l}a<0\\ \frac{a+1}{a}≤\frac{3}{2}\end{array}\right.⇒a<0$,
综上:$a≤\frac{1}{2}$.
(2)存在${x_1},{x_2}∈[{\frac{3}{2},3}]$,使得|h(x1)-h(x2)|≥$\frac{a+1}{2}$成立即:
在$x∈[{\frac{3}{2},3}]$上,h(x)max-h(x)min≥$\frac{a+1}{2}$成立,
因为$h(x)=\frac{f(x)}{x-1}=a({x-1})+\frac{1-a}{x-1}-2$,令$t=x-1∈[{\frac{1}{2},2}]$,
则$g(t)=a•t+\frac{1-a}{t}-2$,$t∈[{\frac{1}{2},2}]$.
(i)当a≤0时,g(t)在$t∈[{\frac{1}{2},2}]$单调递减,所以$g{(t)_{max}}-g{(t)_{min}}≥\frac{a+1}{2}$,
等价于$g({\frac{1}{2}})-g(2)≥\frac{a+1}{2}⇒a≤\frac{2}{7}$,所以a≤0.
(ii)当0<a<1时,$g(t)=a({t+\frac{{\frac{1-a}{a}}}{t}})-2$,g(t)在$({0,\sqrt{\frac{1-a}{a}}}]$上单调递减,
在$[{\sqrt{\frac{1-a}{a}},+∞})$上单调递增.
①当$\sqrt{\frac{1-a}{a}}≤\frac{1}{2}$时,即$\frac{4}{5}≤a<1$,g(t)在$t∈[{\frac{1}{2},2}]$单调递增.
由$g{(t)_{max}}-g{(t)_{min}}≥\frac{a+1}{2}$得到$g(2)-g({\frac{1}{2}})≥\frac{a+1}{2}⇒a≥\frac{4}{5}$,所以$\frac{4}{5}≤a<1$.
②当$\sqrt{\frac{1-a}{a}}≥2$时,$0<a≤\frac{1}{5}$时,g(t)在$t∈[{\frac{1}{2},2}]$单调递减,
由$g{(t)_{max}}-g{(t)_{min}}≥\frac{a+1}{2}$得到$g({\frac{1}{2}})-g(2)≥\frac{a+1}{2}⇒a≤\frac{2}{7}$,所以$0<a≤\frac{1}{5}$.
③当$\frac{1}{2}<\sqrt{\frac{1-a}{a}}<2$,即$\frac{1}{5}<a<\frac{4}{5}$时,$g{(t)_{min}}=g({\sqrt{\frac{1-a}{a}}})$,
最大值则在g(2)与$g({\frac{1}{2}})$中取较大者,作差比较$g(2)-g({\frac{1}{2}})=3a-\frac{3}{2}$,得到分类讨论标准:
a.当$\frac{1}{5}<a<\frac{1}{2}$时,$g(2)-g({\frac{1}{2}})=3a-\frac{3}{2}<0$,此时$g{(t)_{max}}=g({\frac{1}{2}})$,
由$g{(t)_{max}}-g{(t)_{min}}≥\frac{a+1}{2}$,
得到$g({\frac{1}{2}})-g({\sqrt{\frac{1-a}{a}}})≥\frac{a+1}{2}⇒32{a^2}-40a+9≥0⇒a≥\frac{{5+\sqrt{7}}}{8}$或$a≤\frac{{5-\sqrt{7}}}{8}$,
所以$\frac{1}{5}<a≤\frac{{5-\sqrt{7}}}{8}$.
b.当$\frac{1}{2}≤a<\frac{4}{5}$时,$g(2)-g({\frac{1}{2}})=3a-\frac{3}{2}>0$,此时g(t)max=g(2),
由$g{(t)_{max}}-g{(t)_{min}}≥\frac{a+1}{2}$,得到$g(2)-g({\sqrt{\frac{1-a}{a}}})≥\frac{a+1}{2}⇒a≥2\sqrt{a({1-a})}⇒a≥\frac{4}{5}$,
所以此时a∈∅,
在此类讨论中,$a∈({0,\frac{{5-\sqrt{7}}}{8}}]∪[{\frac{4}{5},1})$.
c.当a≥1时,g(t)在$t∈[{\frac{1}{2},2}]$单调递增,由$g{(t)_{max}}-g{(t)_{min}}≥\frac{a+1}{2}$,
得到$g(2)-g({\frac{1}{2}})≥\frac{a+1}{2}⇒a≥\frac{4}{5}$,所以a≥1,
综合以上三大类情况,$a∈({-∞,\frac{{5-\sqrt{7}}}{8}}]∪[{\frac{4}{5},+∞})$.
点评 本题考查函数的单调性的应用,考查存在性问题的解法,注意运用分类讨论的思想方法,以及转化思想,考查运算能力,属于难题.


科目:高中数学 来源: 题型:解答题
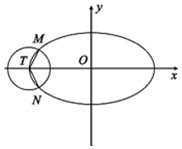 如图已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M,N.
如图已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M,N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,都有x2<1 | B. | ?x∈R,使得x2≥1 | ||
| C. | ?x∈R,都有x≤-1或x≥1 | D. | ?x∈R,使得x2>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{3}{16}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8π | B. | 16π | C. | 32π | D. | 36π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com