
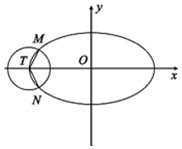
 ��ͼ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$������Բ����TΪԲ����ԲT����x+2��2+y2=r2��r��0������ԲT����ԲC���ڵ�M��N��
��ͼ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$������Բ����TΪԲ����ԲT����x+2��2+y2=r2��r��0������ԲT����ԲC���ڵ�M��N������ ��1��������Բ�������ʹ�ʽ�Ͷ������꣬���a��b��c�Ĺ�ϵ���ɵ���Բ���̣�
��2����M��m��n�����ɶԳ��Կɵ�N��m��-n����������Բ���̣����������������������ʾ��ת��Ϊ����m�Ķ��κ������䷽�������Բ�ķ�Χ���ɵ���Сֵ�������õ�M�����꣬�ɵ�Բ�ķ��̣�
��� �⣺��1��������ɵ�e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$����Բ����T��-2��0����
�ɵ�a=2��c=$\sqrt{3}$��b=$\sqrt{{a}^{2}-{c}^{2}}$=1��
����Բ����Ϊ$\frac{{x}^{2}}{4}$+y2=1��
��2����M��m��n�����ɶԳ��Կɵ�N��m��-n����
����$\frac{{m}^{2}}{4}$+n2=1��
��$\overrightarrow{TM}$•$\overrightarrow{TN}$=��m+2��n��•��m+2��-n��=��m+2��2-n2=��m+2��2-1+$\frac{{m}^{2}}{4}$=$\frac{5}{4}$m2+4m+3
=$\frac{5}{4}$��m+$\frac{8}{5}$��2-$\frac{1}{5}$��
��-2��m��2���ɵ�m=-$\frac{8}{5}$ʱ��$\overrightarrow{TM}$•$\overrightarrow{TN}$����СֵΪ-$\frac{1}{5}$��
��ʱn2=$\frac{9}{25}$��
����r2=��m+2��2+n2=$\frac{13}{25}$��
�ɵ�ԲT�ķ��̣�x+2��2+y2=$\frac{13}{25}$��
���� ���⿼����Բ���̵���ע�����������ʹ�ʽ��������������������Сֵ��ע�����ö��κ�������ֵ����Բ�����ʣ����黯�����������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-3��+�ޣ� | B�� | ��-�ޣ�-3�� | C�� | ��3��+�ޣ� | D�� | ��-�ޣ�3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
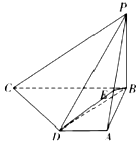 ��ͼ������P-ABCD�У�PB�͵���ABCD��CD��PD������ABCDΪֱ�����Σ�AD��BC��AB��BC��AB=AD=PB=3����E����PA�ϣ���PE=2EA��
��ͼ������P-ABCD�У�PB�͵���ABCD��CD��PD������ABCDΪֱ�����Σ�AD��BC��AB��BC��AB=AD=PB=3����E����PA�ϣ���PE=2EA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
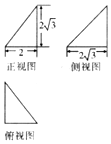
| A�� | $\frac{2��}{3}$ | B�� | $\frac{4��}{3}$ | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 6 | C�� | 9 | D�� | 11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com