
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | 3π | D. | 4π |
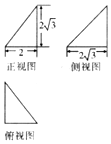
分析 由三视图可知该几何体是一个三棱锥,根据图中数据求出几何体的表面积与体积,
从而求出其内切球的半径r,再计算内切球的表面积.
解答 解:由三视图可知,该几何体是一个三棱锥,
如图所示,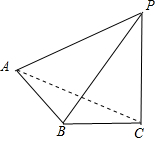
则几何体的表面积为
$S=2×\frac{1}{2}×2×2\sqrt{3}+2×\frac{1}{2}×2\sqrt{3}×4=12\sqrt{3}$,
该几何体的体积为$V=\frac{1}{3}×\frac{1}{2}×2\sqrt{3}×2×2\sqrt{3}=4$;
设其内切球半径为r,则
$V=\frac{1}{3}Sr=4\sqrt{3}r=4$,
求得$r=\frac{{\sqrt{3}}}{3}$,
所以内切球的表面积为
${S_球}=4π{r^2}=4π×{({\frac{{\sqrt{3}}}{3}})^2}=\frac{4π}{3}$.
故选:B.
点评 本题考查了空间几何体三视图的应用问题,也考查了体积与表面积的计算问题,是基础题.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
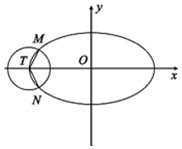 如图已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M,N.
如图已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M,N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在正方形网格纸上,粗实线画出的是某多面体的三视图及其部分尺寸,若该多面体的顶点在同一球面上,则该球的表面积等于( )
如图,在正方形网格纸上,粗实线画出的是某多面体的三视图及其部分尺寸,若该多面体的顶点在同一球面上,则该球的表面积等于( )| A. | 8π | B. | 18π | C. | 24π | D. | 8$\sqrt{6}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
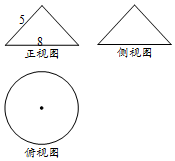 若某几何体的三视图如图所示,其中正视图与侧视图是两个全等的等腰三角形,则此几何体的表面积是( )
若某几何体的三视图如图所示,其中正视图与侧视图是两个全等的等腰三角形,则此几何体的表面积是( )| A. | 36π | B. | 30π | C. | 24π | D. | 15π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | (4,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com