练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．设集合A={x|-x2-x+2＜0}，B={x|2x-5＞0}，则集合A与B的关系是（　　）
    A．B⊆AB．B?AC．B∈AD．A∈B

    分析 化解集合A，B，根据集合之间的关系判断即可．

    解答 解：集合A={x|-x2-x+2＜0}={x|x＞1或x＜-2}，B={x|2x-5＞0}={x|x＞2.5}．
    ∴B⊆A，
    故选A

    点评 本题主要考查集合的基本运算，比较基础

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    5．已知f（x）=ax2-2（a+1）x+3（a∈R）．
    （1）若函数f（x）在$[{\frac{3}{2}，3}]$单调递减，求实数a的取值范围；
    （2）令h（x）=$\frac{f（x）}{x-1}$，若存在${x_1}，{x_2}∈[{\frac{3}{2}，3}]$，使得|h（x1）-h（x2）|≥$\frac{a+1}{2}$成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=|x-2|．
    （1）求不等式f（x）+x2-4＞0的解集；
    （2）设g（x）=-|x+7|+3m，若关于x的不等式f（x）＜g（x）的解集非空，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知$f（x）=\left\{\begin{array}{l}1+x，x∈R\\（1+i）x，x∉R\end{array}\right.$，则f[f（1-i）]等于（　　）
    A．3B．1C．2-iD．3+i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．设$f（x）=\left\{\begin{array}{l}x+4，x≤-2或x≥3\\{x^2}-1，-2＜x＜3\end{array}\right.$，若函数y=f（x）+k的图象与x轴恰有三个不同交点，则k的取值范围是（　　）
    A．（-2，1）B．[0，1]C．[-2，0）D．[-2，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．执行如图所示的程序框图，如果输入N=30，则输出S=（　　）
    A．26B．57C．225D．256

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．某校开展“翻转合作学习法”教学实验，经过一年的实践后，对“翻转班”和“对照班”的全部220名学生的数学学习情况进行测试，按照大于或等于120分为“成绩优秀”，120分以下为“成绩一般”统计，得到如下的2×2列联表．
      成绩优秀 成绩一般 合计
     对照班 20 90 110
     翻转班 40 70 110
     合计 60 160 220
    （Ⅰ）根据上面的列联表判断，能否在犯错误的概率不超过0.001的前提下认为“成绩优秀与翻转合作学习法”有关；
    （Ⅱ）为了交流学习方法，从这次测试数学成绩优秀的学生中，用分层抽样方法抽出6名学生，再从这6名学生中抽3名出来交流学习方法，求至少抽到一名“对照班”学生交流的概率．
    附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$：
     P（K2≥k0） 0.10 0.05 0.025 0.010 0.005 0.001
     k0 2.706 3.841 5.024 6.635 7.879 10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知集合S={1，2}，设S的真子集有m个，则m=（　　）
    A．4B．3C．2D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

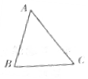    5．为了竖一块广告牌，要制造三角形支架，如图，要求∠ACB=60°，BC的长度大于1米，且AC比AB长0.5米，为了稳固广告牌，要求AC越短越好，则AC最短为（　　）
    A．（1+$\frac{\sqrt{3}}{2}$）米B．2米C．（1+$\sqrt{3}$）米D．（2+$\sqrt{3}$）米

    查看答案和解析>>

    同步练习册答案