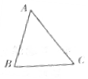Question

5．为了竖一块广告牌，要制造三角形支架，如图，要求∠ACB=60°，BC的长度大于1米，且AC比AB长0.5米，为了稳固广告牌，要求AC越短越好，则AC最短为（　　）

• A． （1+$\frac{\sqrt{3}}{2}$）米
• B． 2米
• C． （1+$\sqrt{3}$）米
• D． （2+$\sqrt{3}$）米

Answer 1

分析 设BC的长度为x米，AC的长度为y米，依据题意可表示出AB的长度，然后代入到余弦定理中求得x和y的关系式，利用基本不等式求得y的最小值，并求得取等号时x的值．

解答 解：设BC的长度为x米，AC的长度为y米，则AB的长度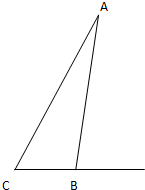为（y-0.5）米，
在△ABC中，依余弦定理得：AB²=AC²+BC²-2AC•BCcos∠ACB，
即（y-0.5）²=y²+x²-2yx×$\frac{1}{2}$，化简，得y（x-1）=x²-$\frac{1}{4}$，
∵x＞1，
∴x-1＞0，
因此y=$\frac{{x}^{2}-\frac{1}{4}}{x-1}$，
y=（x-1）+$\frac{3}{4（x-1）}$+2≥$\sqrt{3}$+2，
当且仅当x-1=$\frac{3}{4（x-1）}$时，取“=”号，
即x=1+$\frac{\sqrt{3}}{2}$时，y有最小值2+$\sqrt{3}$．
故选：D．

点评 本题主要考查了解三角形的实际应用以及基本不等式求最值问题．考查了考生利用数学模型解决实际问题的能力，属于中档题．