
分析 (1)求导,由f′(x)>0则[1,+∞)恒成立,则f(x)在[1,+∞)为增函数,由f(1)=-1<0,f(2)=1>0,函数f(x)在[1,+∞)上有唯一的零点;
(2)求导,分离参数,则a≤$\frac{{x}^{2}(lnx+1)}{x-1}$在[1,+∞)上恒成立,构造辅助函数,求导,由(1)可知,a小于h(x)的x在区间(1,+∞)上的最小值,根据函数的单调性,求得函数的h(x)的最小值的取值范围,即可取得整数a的最大值.
解答 解:(1)由f(x)=(x-2)lnx+2x-3,x≥1,求导f′(x)=lnx-$\frac{2}{x}$+3,(x≥1),
则f′(x)>0恒成立,
则函数f(x)在[1,+∞)为增函数,
由f′(x)≥f′(1)=1,
故f(x)=(x-2)lnx+2x-3在[1,+∞)为增函数,
又由f(1)=-1<0,f(2)=1>0,
∴函数f(x)在[1,+∞)上有唯一的零点;
(2)g(x)=(x-a)lnx+$\frac{a(x-1)}{x}$,g′(x)=lnx+1-$\frac{a}{x}$+$\frac{a}{{x}^{2}}$,在[1,+∞)上恒成立,
由x=1,显然成立,则a≤$\frac{{x}^{2}(lnx+1)}{x-1}$在[1,+∞)上恒成立,
令h(x)=$\frac{{x}^{2}(lnx+1)}{x-1}$,x∈(1,+∞),
则a小于h(x)的x在区间(1,+∞)上的最小值,
求导h′(x)=$\frac{x[(x-2)lnx+2x-3]}{(x-1)^{2}}$,
由(1)可知f(x)=(x-2)lnx+2x-3在[1,+∞)为增函数,
故f(x)在[1,+∞)上由唯一的零点m,
由f(1.60)=0.012,f(1.59)=-0.0086<0,
则m∈(1.59,1.60),f(m)=(m-2)lnm+2m-3=0,则lnm=$\frac{2m-3}{2-m}$,
由当x∈(1,m),h′(x)<0,h(x)在(1,m]为减函数,
x∈(m,+∞),h′(x)>0,h(x)在[m,+∞)为增函数,
故当x=m,h(x)有最小值h(m)=$\frac{{m}^{2}(lnm+1)}{m-1}$=$\frac{{m}^{2}}{2-m}$,
令2-m=t∈(0.4,0.41),则h(x)最小值有,$\frac{{m}^{2}}{2-m}$=$\frac{(2-t)^{2}}{t}$=t+$\frac{4}{t}$-4∈($\frac{41}{100}$+$\frac{236}{41}$,$\frac{32}{5}$)
$\frac{41}{100}$+$\frac{236}{41}$≈6.17,
∴h(x)的最小值大约在6.17~6.4之间,
故整数a的最大值为6.
点评 本题考查导数的综合应用,考查利用导数求函数的单调性及最值,考查函数零点的判断,考查转化思想及构造法的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
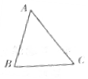 为了竖一块广告牌,要制造三角形支架,如图,要求∠ACB=60°,BC的长度大于1米,且AC比AB长0.5米,为了稳固广告牌,要求AC越短越好,则AC最短为( )
为了竖一块广告牌,要制造三角形支架,如图,要求∠ACB=60°,BC的长度大于1米,且AC比AB长0.5米,为了稳固广告牌,要求AC越短越好,则AC最短为( )| A. | (1+$\frac{\sqrt{3}}{2}$)米 | B. | 2米 | C. | (1+$\sqrt{3}$)米 | D. | (2+$\sqrt{3}$)米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
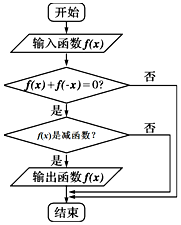 执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )
执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )| A. | f(x)=sinx | B. | f(x)=cosx | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=lg$\frac{1-x}{1+x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-2\sqrt{2},2\sqrt{2}}]$ | B. | [-4,4] | C. | [-5,5] | D. | $[{-5\sqrt{2},5\sqrt{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{12π}$ | B. | $\frac{25}{24π}$ | C. | $\frac{3+\sqrt{3}}{2π}$ | D. | $\frac{3+\sqrt{3}}{4π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-e) | B. | (-∞,-1) | C. | (1,+∞) | D. | (e,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com