Question

8．△ABC中，2$\overrightarrow{OA}$+3$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$，求$\frac{{S}_{△OBC}}{{S}_{△ABC}}$．

Answer 1

分析 延长OB到E，延长OC到F，使得OE=3OB，OF=4OC，以OE，OF为邻边作平行四边形OEDF，用S_△OEF表示出S_△AOC，S_△OAB，S_△OBC，即可得出面积比．

解答 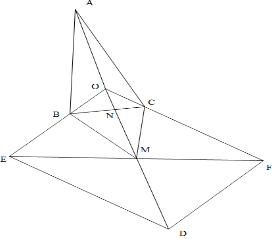解：∵2$\overrightarrow{OA}$+3$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$，
∴3$\overrightarrow{OB}+4\overrightarrow{OC}$=-2$\overrightarrow{OA}$，
延长OB到E，延长OC到F，使得OE=3OB，OF=4OC，
以OE，OF为邻边作平行四边形OEDF，
设OD与EF的交点为M，BC与OM的交点为N，连接BN，CM．
则$\overrightarrow{OD}=\overrightarrow{OE}+\overrightarrow{OF}=3\overrightarrow{OB}+4\overrightarrow{OC}$，
∴$\overrightarrow{OD}=2\overrightarrow{OM}=-2\overrightarrow{OA}$，
∴OA=OM，
∴S_△AOC=S_△OCM=$\frac{1}{4}$S_△OMF=$\frac{1}{8}$S_△OEF，
S_△OAB=S_△OBM=$\frac{1}{3}$S_△OEM=$\frac{1}{6}$S_△OEF，
又S_△OBC=$\frac{1}{2}OB•OC$sin∠BOC=$\frac{1}{2}×$$\frac{1}{3}OE×\frac{1}{4}OF$sin∠BOC=$\frac{1}{12}$S_△OEF，
∴S_△ABC=S_△AOC+S_△OAB+S_△OBC=$\frac{3}{8}$S_△OEF，
∴$\frac{{S}_{△OBC}}{{S}_{△ABC}}$=$\frac{\frac{1}{12}}{\frac{3}{8}}$=$\frac{2}{9}$．

点评 本题考查了平面向量的几何运算，三角形的面积计算，属于中档题．