
分析 若y=f(x)图象有两条对称轴x=a,x=b,(a≠b),则y=f(x)必是周期函数,且一周期为2|a-b|,根据函数的对称性和周期性,可证得结论.
解答 解:若y=f(x)图象有两条对称轴x=a,x=b,(a≠b),
则y=f(x)必是周期函数,且一周期为2|a-b|,
理由如下:
由已知可得:f(x)=f(2a-x),且f(x)=f(2b-x),
不妨令a>b,
则f[x+(2a-2b)]=f(2a-x-2a+2b)=f(2b-x)=f(x),
即此时y=f(x)的周期为2a-2b;
同理可得:a<b时,y=f(x)的周期为2b-2a;
综上可得:y=f(x)的周期为2|a-b|.
故答案为:2|a-b|
点评 本题考查的知识点是抽象函数的周期性和对称性,难度中档.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{6}$=1 | C. | $\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{5}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
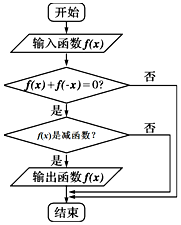 执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )
执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )| A. | f(x)=sinx | B. | f(x)=cosx | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=lg$\frac{1-x}{1+x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-2\sqrt{2},2\sqrt{2}}]$ | B. | [-4,4] | C. | [-5,5] | D. | $[{-5\sqrt{2},5\sqrt{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com