
分析 (1)由题意,数列{bn},{cn}为递增数列,即可求出{bn},{cn}的通项公式
(2)由题意可得,k-4<0,且判别式(k-6)2+8(k-4)≤0,解不等式可得k=2,可得f(x)的解析式,可得f(n)=-2n2+2n,代值计算即可求出g(n)
的表达式,根据g(n)=$\frac{2}{1-2n}$为关于n的单调递增函数,即可求出最小值.
(3)假设存在非零整数λ.运用构造数列,结合等比数列的定义和通项公式和求和公式,化简所求不等式,即为2n-1>(-1)n-1λ恒成立,讨论n为奇数和偶数,即可得到所求.
解答 解:(1)数列{bn}为递增数列,则|bn+1-bn|=bn+1-bn=2,
∴{bn}为公差d=2的等差数列b1=1.
∴bn=1+(n-1)×2=2n-1(n∈N*)
由cn+12=4cn2,
∴$\frac{{C}_{n+1}^{2}}{{C}_{n}^{2}}$=4
又∵数列{cn}为递增数列,
∴$\frac{{c}_{n+1}}{{c}_{n}}$=2,
∴数列{cn} 公比q=2的等比数列,首先c1=-1,
∴cn=(-1)•2n-1=-2n-1,(n∈N*)
(2)对任意实数x,有f(x)≤6x+2恒成立,
即为(k-4)x2+(k-6)x-2≤0,
k-4<0,且判别式(k-6)2+8(k-4)≤0,即为k2-4k+4≤0,
即(k-2)2≤0,解得k=2,
即有f(x)=-2x2+2x,
∴f(n)=-2n2+2n,
∴g(n)=$\frac{{b}_{n}}{f(n)-\frac{1}{2}}$=$\frac{2n-1}{-2{n}^{2}+2n-\frac{1}{2}}$=$\frac{4n-2}{-4{n}^{2}+4n-1}$=2•$\frac{2n-1}{(1-2n)(2n-1)}$=$\frac{2}{1-2n}$
∴g(n)=$\frac{2}{1-2n}$为关于n的单调递增函数,又∵n≥1.
∴g(n)min=g(1)=$\frac{2}{1-2}$=-2
(3)由(2)得f(x)=-2x2+2x=-2(x-$\frac{1}{2}$)2+$\frac{1}{2}$
∵an+1=f(an),
又∵f(x)≤$\frac{1}{2}$,
∴正项数列{an}满足an∈(0,$\frac{1}{2}$]
令bn=$\frac{1}{2}$-an,则bn+1=$\frac{1}{2}$-an+1=$\frac{1}{2}$-(-2an2+2an)=2($\frac{1}{2}$-an)2,
∴lgbn+1=lg2($\frac{1}{2}$-an)2=lg2+2lg($\frac{1}{2}$-an)=lg2+2lgbn,
∴lgbn+1+lg2=2(lg2+lgbn),
∵lg2+lgb1=lg($\frac{1}{2}$-$\frac{1}{3}$)+lg2=lg$\frac{1}{3}$
∴lg2+lgbn=(lg$\frac{1}{3}$)•2n-1,
∴lg2bn=lg($\frac{1}{3}$)${\;}^{{2}^{n-1}}$,
∴bn=$\frac{1}{2}$•($\frac{1}{3}$)${\;}^{{2}^{n-1}}$,
∴log3($\frac{1}{\frac{1}{2}-{a}_{1}}$)+log3($\frac{1}{\frac{1}{2}-{a}_{2}}$)+…+log3($\frac{1}{\frac{1}{2}-{a}_{n}}$)=log32•${3}^{{2}^{0}}$+log32•3${\;}^{{2}^{1}}$+…+log32•3${\;}^{{2}^{n-1}}$
=nlog32+$\frac{{2}^{n}(1-{2}^{n})}{1-2}$=nlog32+2n-1,
要证2n+nlog32-1>-1+(-1)n-1•2+nlog32恒成立
即证2n>(-1)n-12λ恒成立
∴2n>(-1)n-12λ恒成立
①当n为奇数时,即λ<2n-1恒成立,当且仅当n=1时,2n-1有最小值1为.∴λ<1;
②当n为偶数时,即λ>-2n-1恒成立,当且仅当n=2时,有最大值-2为.∴λ>-2,
所以,对任意n∈N*,有-2<λ<1.又λ为非零整数,
∴λ=-1.
点评 本题考查二次函数的解析式和值域的求法,同时考查等比数列的定义和通项公式,考查不等式的恒成立问题转化为求最值问题,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
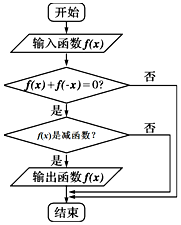 执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )
执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx,②f(x)=cosx,③f(x)=$\frac{1}{x}$,④f(x)=lg$\frac{1-x}{1+x}$,则输出的函数是( )| A. | f(x)=sinx | B. | f(x)=cosx | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=lg$\frac{1-x}{1+x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{12π}$ | B. | $\frac{25}{24π}$ | C. | $\frac{3+\sqrt{3}}{2π}$ | D. | $\frac{3+\sqrt{3}}{4π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com