Question

10．若实数x、y满足$\left\{\begin{array}{l}{-2x+1≤y≤2x-1}\\{0＜x≤3}\end{array}\right.$，则x-2y的取值范围是[-7，13]．

Answer 1

分析 作出题中不等式组表示的平面区域，得如图的△ABC及其内部，再将目标函数z=x-2y对应的直线进行平移，求出最优解，可得x-2y的取值范围．

解答 解：作出不等式组$\left\{\begin{array}{l}{-2x+1≤y≤2x-1}\\{0＜x≤3}\end{array}\right.$，表示的平面区域：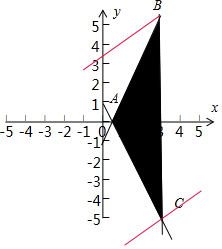

得到如图的△ABC及其内部，其中A（$\frac{1}{2}$，0），B（3，5），C（3，-5）
设z=F（x，y）=x-2y，将直线l：z=x-2y进行平移，
当l经过点B时，目标函数z达到最大值，得z_最大值=F（3，-5）=13；
当l经过点A时，目标函数z达到最小值，得z_最小值=F（3，5）=-7
因此，x+2y的取值范围是[-7，13]．
故答案为：[-7，13]．

点评 本题给出二元一次不等式组，求目标函数z=x-2y的取值范围，着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识，属于中档题．