
| ��λְ���ijɼ����֣� | 87 | 88 | 91 | 91 | 93 |
| �ҵ�λְ���ijɼ����֣� | 85 | 89 | 91 | 92 | 93 |
���� ��1��������ס���������λְ���Ŀ��Գ�����ƽ�������Լ����ǵķ����С�ĸ��ȶ���
��2�����ҵ�λ��ȡ����ְ���ķ��������л����¼����оٷ���ù�10���������ȡ������ְ���ķ�����ֵ������4���¼����оٷ���ù���5�����ɹŵ����ʽ��ó�ȡ������ְ���ķ���֮��ľ���ֵ������4�ĸ��ʣ�
��� �⣺��I��${\overline x_��}=\frac{1}{5}��87+88+91+91+93��=90$��
${\overline x_��}=\frac{1}{5}��85+89+91+92+93��=90$����2�֣�
${s^2}_��=\frac{1}{5}[{��87-90��^2}+{��88-90��^2}+��91-90{��^2}+��91-90{��^2}+��93-90{��^2}]=\frac{24}{5}$��
${s^2}_��=\frac{1}{5}[{��85-90��^2}+{��89-90��^2}+��91-90{��^2}+��92-90{��^2}+��93-90{��^2}]=8$����4�֣�
��$\frac{24}{5}��8$�����λְ���Է���֪ʶ�����ո�Ϊ�ȶ�����5�֣�
��II�����ȡ��2��ְ���ijɼ�ֻ��ľ���ֵ�����ǣ�4�֣�Ϊ�¼�A��
���л����¼��У���85��89������85��91������85��92����85��93������89��85����
��89��91������89��92������89��93������91��85������91��89������91��92����
��91��93������92��85������92��89������92��91����92��93������93��85����
��93��89������93��91������93��92������20������8�֣�
�¼�A�����Ļ����¼��У�
��85��89������85��91������85��92������85��93������89��85������89��93����
��91��85������92��85������93��85������93��89������10������10�֣�
��$P��A��=\frac{10}{20}=\frac{1}{2}$����12�֣�
���� ������Ҫ����ƽ�����ͷ���Ķ����������оٷ���������оٳ������¼��������������¼����ŵ���ʵļ��㹫ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
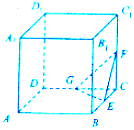 ��ͼ��ʾ��������ABCD-A1B1C1D1���ⳤΪ1��E��F��G�ֱ�����BC��CC1��CD���е㣬ƽ�������B1����ƽ��EFGƽ�У���ƽ���������������������صõĽ���Բ�����ΪΪ$\frac{2}{3}��$��
��ͼ��ʾ��������ABCD-A1B1C1D1���ⳤΪ1��E��F��G�ֱ�����BC��CC1��CD���е㣬ƽ�������B1����ƽ��EFGƽ�У���ƽ���������������������صõĽ���Բ�����ΪΪ$\frac{2}{3}��$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��2����-1��-2�� | B�� | ��1��2����1��-2�� | C�� | ��1��2�� | D�� | ��1��-2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 140�� | B�� | 80�� | C�� | 70�� | D�� | 35�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com