
| 喜欢吃辣 | 不喜欢吃辣 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
| p(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)计算对于的数据,补充出2×2列联表即可;(2)计算k2的值,从而判断结论即可.
解答 解:(1)∵在全部100人中随机抽取1人抽到喜欢吃辣的学生的概率为$\frac{3}{5}$.
∴在100人中,喜欢吃辣的有$\frac{3}{5}×100=60$,∴男生喜欢吃辣的有60-20=40,
列表补充如下:
| 喜欢吃辣 | 不喜欢吃辣 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
点评 本题考查了独立性检验,考查计算能力,是一道基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x3•x2=x5 | B. | x+x2=x3 | C. | 2x3÷x2=x | D. | ($\frac{x}{2}$)3=$\frac{{x}^{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 16 | 22 | 77 | 94 | 39 | 49 | 54 | 43 | 54 | 82 | 17 | 37 | 93 | 23 | 78 | 87 | 35 | 20 | 96 | 43 |
| 84 | 42 | 17 | 53 | 31 | 57 | 24 | 55 | 06 | 88 | 77 | 04 | 74 | 47 | 67 | 21 | 76 | 33 | 50 | 25 |
| A. | 23 | B. | 37 | C. | 35 | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
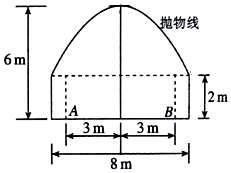 如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,已知行车道总宽度|AB|=6米,那么车辆通过隧道的限制高度是多少米?
如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,已知行车道总宽度|AB|=6米,那么车辆通过隧道的限制高度是多少米?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{5}{9}$ | C. | $\frac{7}{9}$ | D. | $\frac{5}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com