
【题目】已知椭圆C: ![]() =1的左顶点为A(﹣3,0),左焦点恰为圆x2+2x+y2+m=0(m∈R)的圆心M.
=1的左顶点为A(﹣3,0),左焦点恰为圆x2+2x+y2+m=0(m∈R)的圆心M.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点A且与圆M相切于点B的直线,交椭圆C于点P,P与椭圆C右焦点的连线交椭圆于Q,若三点B,M,Q共线,求实数m的值.
【答案】解:(Ⅰ)圆M方程变形得:(x+1)2+y2=1﹣m,即M(﹣1,0),∴c=1,
∵顶点A(﹣3,0),∴a=3,
∴b2=a2﹣c2=9﹣1=8,
则椭圆C的方程为 ![]() =1;
=1;
(Ⅱ)设AP方程为x=ty﹣3(t≠0),代入椭圆方程得:(8t2+9)y2﹣48ty=0,
解得:yA=0,yP= ![]() ,
,
∴xP=tyP﹣3= ![]() ,
,
∵右焦点坐标为(1,0),
∴PQ方程为x= ![]() y+1,代入椭圆方程得:
y+1,代入椭圆方程得: ![]() y2+
y2+ ![]() y﹣64=0,
y﹣64=0,
∴yPyQ=  ,即yQ=
,即yQ= ![]() ,
,
∴xQ= ![]() yQ+1=
yQ+1= ![]() ,
,
由B,M,Q三点共线,可得MQ⊥AP,即kMQkAP=﹣1,
∴ ![]() =﹣1,
=﹣1,
解得:t=± ![]() ,
,
∴直线AP方程为x=± ![]() y﹣3,
y﹣3,
则圆心M到AP的距离为1,即圆半径为 ![]() =1,
=1,
则m=0
【解析】(Ⅰ)圆M方程变形找出M坐标,确定出c的值,由顶点A坐标确定出a的值,进而求出b的值,即可确定出椭圆C的方程;(Ⅱ)设AP方程为x=ty﹣3(t≠0),代入椭圆方程,消去x表示出P的纵坐标,进而表示出横坐标,再表示出Q坐标,根据B,M,Q三点共线,得到MQ与AP垂直,即直线MQ与直线AP斜率乘积为﹣1,求出t的值,确定出直线AP方程,进而求出m的值.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=xln(ax+1)(a≠0).
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若a>0且满足:对x1 , x2∈[﹣1,1],都有|f(x1)﹣f(x2)|≤ln3﹣ln2,试比较ea﹣1与 ![]() 的大小,并证明.
的大小,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校矩形的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在![]() 范围内,规定分数在80以上(含80)的同学获奖,按文理科用分层抽样的放发抽取200人的成绩作为样本,得到成绩的频率分布直方图.
范围内,规定分数在80以上(含80)的同学获奖,按文理科用分层抽样的放发抽取200人的成绩作为样本,得到成绩的频率分布直方图.
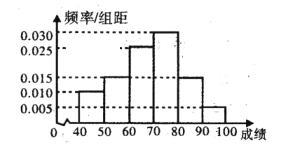
(Ⅰ)填写下面![]() 的列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”;
的列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”;
(Ⅱ)将上述调查所得的频率视为概率,现从参赛学生中,任意抽取3名学生,记“获奖”学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.

附表及公式:![]() ,其中
,其中![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]()
![]() ,其中向量
,其中向量 ![]() =(2cosx,1),
=(2cosx,1), ![]() =(cosx,
=(cosx, ![]() sin2x),x∈R.
sin2x),x∈R.
(1)求f(x)的最小正周期与单调递减区间;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,已知f(A)=2,b=1,△ABC的面积为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且a1=1,an+1=![]() Sn(n=1,2,3,…).
Sn(n=1,2,3,…).
(1)求数列{an}的通项公式;
(2)当bn=![]() (3an+1)时,求证:数列
(3an+1)时,求证:数列![]() 的前n项和Tn=
的前n项和Tn=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数:f(x)=﹣x3﹣3x2+(1+a)x+b(a<0,b∈R).
(1)令h(x)=f(x﹣1)﹣b+a+3,判断h(x)的奇偶性,并讨论h(x)的单调性;
(2)若g(x)=|f(x)|,设M(a,b)为g(x)在[﹣2,0]的最大值,求M(a,b)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)求第3,4,5组的频率;
(2)为了了解最优秀学生的情况,该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com