
| A. | $\frac{2}{3}$或$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{3}{2}$或2 |
分析 讨论x-2a在区间[1,4]上恒大于零,恒小于零,既有大于零又有小于零.对应的f(x)的最大值是什么,求出a的值.
解答 解:(1)当x-2a在区间[1,4]上恒大于零时,
由x-2a>0,可得a<$\frac{x}{2}$;
当x=1时,满足x-2a在[1,4]上恒大于零,即a<$\frac{1}{2}$;
此时函数f(x)=$\frac{x-2a}{x+2a}$=1-$\frac{4a}{x+2a}$,
该函数在定义域[1,4]上为增函数,在x=4时,取最大值f(4)=$\frac{1}{2}$,
∴a=$\frac{2}{3}$,不满足a<$\frac{1}{2}$的假设,舍去.
(2)当x-2a在区间[1,4]上恒小于零时,
∵x-2a<0,∴a>$\frac{x}{2}$;
当x=4时,满足x-2a在[1,4]上恒小于零,即a>2;
此时函数f(x)=$\frac{-(x-2a)}{x+2a}$=$\frac{4a}{x+2a}$-1,
该函数在定义域[1,4]上为减函数,在x=1时,取最大值f(1)=$\frac{1}{2}$,
∴a=$\frac{3}{2}$,不满足a>2的假设,舍去.
(3)由前面讨论知,当$\frac{1}{2}$<a<2时,x-2a在区间[1,4]上既有大于零又有小于零时,
①当x<2a时,x-2a<0,此时函数f(x)=$\frac{4a}{x+2a}$-1在[1,2a)上为减函数,
在x=1时,取到最大值f(1)=$\frac{1}{2}$;
②当x>2a时,x-2a>0.此时函数f(x)=1-$\frac{4a}{x+2a}$在(2a,4]时为增函数,
在x=4时,取到最大值f(4)=$\frac{1}{2}$;
总之,此时函数在区间[1,4]上先减后增,在端点处取到最大值;
当函数在x=1处取最大值时,解得a=$\frac{3}{2}$,此时函数f(x)=$\frac{|x-3|}{x+3}$,
将函数的另一个最大值点x=4代入得:f(4)=$\frac{1}{7}$,
∵f(1)>f(4),∴满足条件;
当函数在x=4处取最大值时,解得a=$\frac{2}{3}$,此时函数f(x)=$\frac{|x-\frac{4}{3}|}{x+\frac{4}{3}}$,
将函数的另一个最大值点x=1代入得:f(1)=$\frac{1}{7}$,
∵f(1)<f(4),∴满足条件;
∴a=$\frac{2}{3}$或a=$\frac{3}{2}$;
故选:A.
点评 本题考查了含有绝对值的函数在某一闭区间上的最值问题,注意运用分类讨论的思想方法,运用单调性解决,是易错题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,6] | B. | [1,6) | C. | (2,4] | D. | (2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>1或-1<x<0} | B. | {x|x>1或x<-1} | C. | {x|0<x<1或x<-1} | D. | {x|-1<x<1且x≠0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
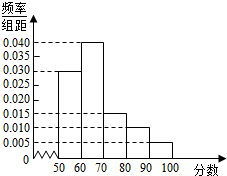 根据某组调查数据制作的频率分布直方图如图所示,则该组数据中的数位于区间(60,70)内的频率是( )
根据某组调查数据制作的频率分布直方图如图所示,则该组数据中的数位于区间(60,70)内的频率是( )| A. | 0.004 | B. | 0.04 | C. | 0.4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {1,2} | C. | {0} | D. | 以上答案都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com