
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,离心率为
,离心率为![]() ;圆
;圆![]() 过椭圆
过椭圆![]() 的三个顶点.过点
的三个顶点.过点![]() 且斜率不为0的直线
且斜率不为0的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)证明:在![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() 为定值;并求出该定点的坐标.
为定值;并求出该定点的坐标.
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】过去大多数人采用储蓄的方式将钱储蓄起来,以保证自己生活的稳定,考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式,随着金融业的发展,普通人能够使用的投资理财工具也多了起来,为了研究某种理财工具的使用情况,现对![]() 年龄段的人员进行了调查研究,将各年龄段人数分成5组,
年龄段的人员进行了调查研究,将各年龄段人数分成5组,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并整理得到频率分布直方图:
,并整理得到频率分布直方图:
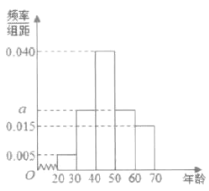
(Ⅰ)求图中的![]() 值;
值;
(Ⅱ)求被调查人员的年龄的中位数和平均数;
(Ⅲ)采用分层抽样的方法,从第二组、第三组、第四组中共抽取8人,在抽取的8人中随机抽取2人,则这2人都来自于第三组的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某环线地铁按内、外环线同时运行,内、外环线的长均为30千米(忽略内、外环线长度差异).
(1)当9列列车同时在内环线上运行时,要使内环线乘客最长候车时间为10分钟,求内环线列车的最小平均速度;
(2)新调整的方案要求内环线列车平均速度为25千米/小时,外环线列车平均速度为30千米/小时.现内、外环线共有18列列车全部投入运行,要使内外环线乘客的最长候车时间之差不超过1分钟,向内、外环线应各投入几列列车运行?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型工厂有![]() 台大型机器,在
台大型机器,在![]() 个月中,
个月中,![]() 台机器至多出现
台机器至多出现![]() 次故障,且每台机器是否出现故障是相互独立的,出现故障时需
次故障,且每台机器是否出现故障是相互独立的,出现故障时需![]() 名工人进行维修.每台机器出现故障的概率为
名工人进行维修.每台机器出现故障的概率为![]() .已知
.已知![]() 名工人每月只有维修
名工人每月只有维修![]() 台机器的能力,每台机器不出现故障或出现故障时有工人维修,就能使该厂获得
台机器的能力,每台机器不出现故障或出现故障时有工人维修,就能使该厂获得![]() 万元的利润,否则将亏损
万元的利润,否则将亏损![]() 万元.该工厂每月需支付给每名维修工人
万元.该工厂每月需支付给每名维修工人![]() 万元的工资.
万元的工资.
(1)若每台机器在当月不出现故障或出现故障时有工人进行维修,则称工厂能正常运行.若该厂只有![]() 名维修工人,求工厂每月能正常运行的概率;
名维修工人,求工厂每月能正常运行的概率;
(2)已知该厂现有![]() 名维修工人.
名维修工人.
(ⅰ)记该厂每月获利为![]() 万元,求
万元,求![]() 的分布列与数学期望;
的分布列与数学期望;
(ⅱ)以工厂每月获利的数学期望为决策依据,试问该厂是否应再招聘![]() 名维修工人?
名维修工人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人的月工资由基础工资和绩效工资组成2010年每月的基础工资为2100元、绩效工资为2000元从2011年起每月基础工资比上一年增加210元、绩效工资为上一年的![]() 照此推算,此人2019年的年薪为______万元(结果精确到
照此推算,此人2019年的年薪为______万元(结果精确到![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若函数
,若函数![]() 是增函数,则称函数
是增函数,则称函数![]() 具有性质A.
具有性质A.
![]() 若
若![]() ,求
,求![]() 的解析式,并判断
的解析式,并判断![]() 是否具有性质A;
是否具有性质A;
![]() 判断命题“减函数不具有性质A”是否真命题,并说明理由;
判断命题“减函数不具有性质A”是否真命题,并说明理由;
![]() 若函数
若函数![]() 具有性质A,求实数k的取值范围,并讨论此时函数
具有性质A,求实数k的取值范围,并讨论此时函数![]() 在区间
在区间![]() 上零点的个数.
上零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有9个大小形状完全相同的球,球的编号分别为1,2,…,9,随机摸出两个球,则两个球的编号之和大于9的概率是______(结果用分数表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某热力公司每年燃料费约24万元,为了“环评”达标,需要安装一块面积为![]() (
(![]() )(单位:平方米)可用15年的太阳能板,其工本费为
)(单位:平方米)可用15年的太阳能板,其工本费为![]() (单位:万元),并与燃料供热互补工作,从此,公司每年的燃料费为
(单位:万元),并与燃料供热互补工作,从此,公司每年的燃料费为![]() (
(![]() 为常数)万元,记
为常数)万元,记![]() 为该公司安装太阳能板的费用与15年的燃料费之和.
为该公司安装太阳能板的费用与15年的燃料费之和.
(1)求![]() 的值,并建立
的值,并建立![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求![]() 的最小值,并求出此时所安装太阳能板的面积.
的最小值,并求出此时所安装太阳能板的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com