
 《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( )
《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( )| A. | 100πcm3 | B. | $\frac{500π}{3}c{m^3}$ | C. | 400πcm3 | D. | $\frac{4000π}{3}c{m^3}$ |
分析 如图所示,该几何体为四棱锥P-ABCD.底面ABCD为矩形,其中PD⊥底面ABCD.
解答 解:如图所示,该几何体为四棱锥P-ABCD.底面ABCD为矩形,其中 PD⊥底面ABCD.
PD⊥底面ABCD.
AB=6,AD=2$\sqrt{7}$,PD=6.
则该阳马的外接球的直径为PB=$\sqrt{P{D}^{2}+D{B}^{2}}$
=$\sqrt{P{D}^{2}+A{D}^{2}+A{B}^{2}}$=$\sqrt{{6}^{2}+{6}^{2}+(2\sqrt{7})^{2}}$=10.
∴该阳马的外接球的体积=$\frac{4π×{5}^{3}}{3}$=$\frac{500π}{3}$cm3.
故选:B.
点评 本题考查了四棱锥的三视图、长方体的性质、球的体积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (1,0),(0,-2) | B. | (0,1),(-1,0) | C. | (0,-1),(1,0) | D. | (0,3),(-3,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2π | B. | $\frac{3π}{2}$ | C. | $\frac{4π}{3}$ | D. | $\frac{7π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
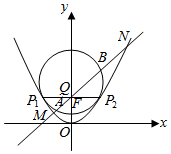 如图,抛物线C:x2=2py(p>0)的准线为y=-1,取过焦点F且平行于x轴的直线与抛物线交于不同的两点P1,P2,过P1,P2作圆心为Q的圆,使抛物线上其余点均在圆外,且∠P1QP2=90°.
如图,抛物线C:x2=2py(p>0)的准线为y=-1,取过焦点F且平行于x轴的直线与抛物线交于不同的两点P1,P2,过P1,P2作圆心为Q的圆,使抛物线上其余点均在圆外,且∠P1QP2=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com