
分析 (1)把已知递推式变形,可得$\frac{1}{{a}_{n+1}-1}=-\frac{2}{{a}_{n}-1}-1$.令$\frac{1}{{a}_{n}-1}={c}_{n}$,则${c}_{n+1}+\frac{1}{3}=-2({c}_{n}+\frac{1}{3})$.得数列{${c}_{n}+\frac{1}{3}$}是以$\frac{4}{3}$为首项,以-2为公比的等比数列,求其通项公式,可得an-1,an+2,代入bn=$\frac{{a}_{n}-1}{{a}_{n}+2}$求数列{bn}的通项公式;
(2)由(1)知,数列{bn}是以$\frac{1}{4}$为首项,以$-\frac{1}{2}$为公比的等比数列,求其前n项和,代入bnSn,对n分类利用数列的函数特性证得bnSn≤$\frac{1}{16}$.
解答 解:(1)由an+1=$\frac{2}{{a}_{n}+1}$,得${a}_{n+1}-1=\frac{2}{{a}_{n}+1}-1=\frac{2-{a}_{n}-1}{{a}_{n}+1}=-\frac{{a}_{n}-1}{{a}_{n}+1}$,
∴$\frac{1}{{a}_{n+1}-1}=-\frac{{a}_{n}+1}{{a}_{n}-1}=-\frac{{a}_{n}-1+2}{{a}_{n}-1}=-\frac{2}{{a}_{n}-1}-1$.
令$\frac{1}{{a}_{n}-1}={c}_{n}$,则cn+1=-2cn-1,即${c}_{n+1}+\frac{1}{3}=-2({c}_{n}+\frac{1}{3})$.
又${c}_{1}+\frac{1}{3}=\frac{1}{{a}_{1}-1}+\frac{1}{3}=\frac{4}{3}$,
∴数列{${c}_{n}+\frac{1}{3}$}是以$\frac{4}{3}$为首项,以-2为公比的等比数列,
则${c}_{n}+\frac{1}{3}=\frac{4}{3}•(-2)^{n-1}$,
∴${c}_{n}=-\frac{1}{3}+\frac{4}{3}•(-2)^{n-1}$,即$\frac{1}{{a}_{n}-1}=-\frac{1}{3}+\frac{4}{3}•(-2)^{n-1}$.
∴${a}_{n}-1=\frac{1}{-\frac{1}{3}+\frac{4}{3}•(-2)^{n-1}}$,${a}_{n}+2=\frac{1}{-\frac{1}{3}+\frac{4}{3}•(-2)^{n-1}}+3=\frac{1-1+4•(-2)^{n-1}}{-\frac{1}{3}+\frac{4}{3}•(-2)^{n-1}}$,
则bn=$\frac{{a}_{n}-1}{{a}_{n}+2}$=$\frac{1}{4•(-2)^{n-1}}=(-1)^{n-1}•\frac{1}{{2}^{n+1}}=\frac{1}{(-2)^{n+1}}$;
证明:(2)由(1)知,数列{bn}是以$\frac{1}{4}$为首项,以$-\frac{1}{2}$为公比的等比数列,
则${S}_{n}=\frac{\frac{1}{4}[1-(-\frac{1}{2})^{n}]}{1+\frac{1}{2}}=\frac{1}{6}[1-(-\frac{1}{2})^{n}]$,
∴bnSn=$(-\frac{1}{2})^{n+1}•\frac{1}{6}[1-(-\frac{1}{2})^{n}]$.
当n为偶数时,bnSn<0;
当n为奇数时,函数bnSn为减函数,
∴bnSn≤b1S1=$\frac{1}{4}×\frac{1}{6}×\frac{3}{2}=\frac{1}{16}$.
综上,bnSn≤$\frac{1}{16}$(n∈N*).
点评 本题考查数列递推式,训练了利用构造等比数列求数列的通项公式,训练了利用数列的单调性求最值,是中档题.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,e2) | D. | (e2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
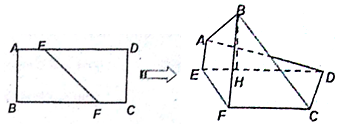
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( )
《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( )| A. | 100πcm3 | B. | $\frac{500π}{3}c{m^3}$ | C. | 400πcm3 | D. | $\frac{4000π}{3}c{m^3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 664 | B. | 844 | C. | 968 | D. | 1204 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
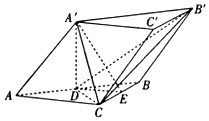 在斜三棱柱ABC-A′B′C′中,AC=BC=A′A=A′C,A′在底面ABC上的射影为AB的中点D,E为线段BC的中点.
在斜三棱柱ABC-A′B′C′中,AC=BC=A′A=A′C,A′在底面ABC上的射影为AB的中点D,E为线段BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com