
已知函数f(x)=(x-a)2(x-b)(a,b∈R,a<b).
(1)当a=1,b=2时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)设x1,x2是f(x)的两个极值点,x3是f(x)的一个零点,且x3≠x1,x3≠x2.证明:存在实数x4,使得x1,x2,x3,x4按某种顺序排列后构成等差数列,并求x4.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
设抛物线C:y2=4x的焦点为F,直线l过F且与C交于A,B两点.若|AF|=3|BF|,则l的方程为( )
(A)y=x-1或y=-x+1
(B)y=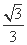 (x-1)或y=-
(x-1)或y=-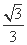 (x-1)
(x-1)
(C)y=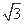 (x-1)或y=-
(x-1)或y=-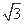 (x-1)
(x-1)
(D)y=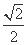 (x-1)或y=-
(x-1)或y=-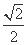 (x-1)
(x-1)
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.

(1)证明:C,B, D,E四点共圆;
(2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
直线与双曲线位置关系的判定及应用
已知双曲线C的方程为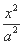 -
-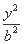 =1(a>0,b>0),离心率e=
=1(a>0,b>0),离心率e=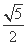 ,顶点到渐近线的距离为
,顶点到渐近线的距离为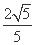 .
.
(1)求双曲线C的方程;
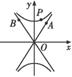
(2)如图,P是双曲线C上一点,A、B两点在双曲线C的两条渐近线上,且分别位于第一、二象限.
若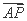 =λ
=λ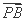 ,λ∈
,λ∈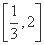 .求△AOB的面积的取值范围.
.求△AOB的面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com