
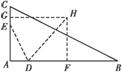
如图所示,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.

(1)证明:C,B, D,E四点共圆;
(2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.
(1)证明:连接DE,根据题意在△ADE和△ACB中,
AD·AB=mn=AE·AC,
即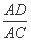 =
=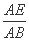 .
.
又∠DAE=∠CAB,从而△ADE∽△ACB,
因此∠ADE=∠ACB,
∴∠ACB+∠EDB=180°,
∴C、B、D、E四点共圆.
(2)解:m=4,n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12,故AD=2,AB=12.
取CE的中点G,DB的中点F,分别过G、F作AC、AB的垂线,两垂线相交于H点,连接DH.
因为C、B、D、E四点共圆,
∴C、B、D、E四点所在圆的圆心为H,半径为DH.
由于∠A=90°,故GH∥AB,HF∥AC,
从而HF=AG=5,DF=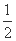 ×(12-2)=5,
×(12-2)=5,
故C、B、D、E四点所在圆的半径为5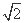 .
.


科目:高中数学 来源: 题型:
已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为( )
(A) (B)1 (C)
(B)1 (C) 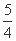 (D)
(D)
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于点D.过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,EF= ,则线段CD的长为 .
,则线段CD的长为 .

查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=(x-a)2(x-b)(a,b∈R,a<b).
(1)当a=1,b=2时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)设x1,x2是f(x)的两个极值点,x3是f(x)的一个零点,且x3≠x1,x3≠x2.证明:存在实数x4,使得x1,x2,x3,x4按某种顺序排列后构成等差数列,并求x4.
查看答案和解析>>
科目:高中数学 来源: 题型:
过双曲线C: 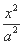 -
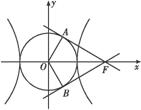
-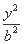 =1(a>0,b>0)的一个焦点作圆x2+y2=a2的两条切线,切点分别为A、B.若∠AOB=120°(O是坐标原点),则双曲线C的离心率为 .
=1(a>0,b>0)的一个焦点作圆x2+y2=a2的两条切线,切点分别为A、B.若∠AOB=120°(O是坐标原点),则双曲线C的离心率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com