
直线与双曲线位置关系的判定及应用
已知双曲线C的方程为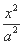 -
-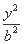 =1(a>0,b>0),离心率e=
=1(a>0,b>0),离心率e=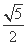 ,顶点到渐近线的距离为
,顶点到渐近线的距离为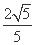 .
.
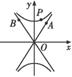
(1)求双曲线C的方程;
(2)如图,P是双曲线C上一点,A、B两点在双曲线C的两条渐近线上,且分别位于第一、二象限.
若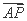 =λ
=λ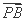 ,λ∈
,λ∈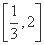 .求△AOB的面积的取值范围.
.求△AOB的面积的取值范围.
解:(1)由题意知,双曲线C的顶点(0,a)到渐近线ax-by=0的距离为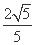 ,
,
∴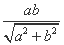 =
=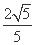 ,即
,即 =
=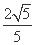 .
.
由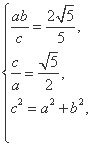 得
得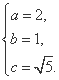
∴双曲线C的方程为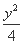 -x2=1.
-x2=1.
(2)由(1)知双曲线C的两条渐近线方程为y=±2x,
设A(m,2m),B(-n,2n),m>0,n>0.
由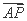 =λ
=λ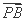 得P点坐标为
得P点坐标为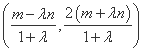 ,
,
将P点坐标代入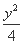 -x2=1,化简得mn=
-x2=1,化简得mn=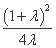 .
.
设∠AOB=2θ,∵tan(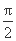 -θ)2.
-θ)2.
∴tan θ=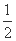 ,sin 2θ=
,sin 2θ=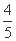 .
.
又|OA|=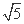 m,|OB|=
m,|OB|=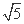 n,
n,
∴S△AOB=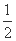 |OA|·|OB|·sin 2θ
|OA|·|OB|·sin 2θ
=2mn
=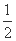
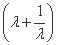 +1,
+1,
记S(λ)= 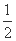
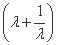 +1,λ∈
+1,λ∈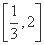 .
.
则S′(λ)= 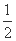
 .
.
由S′(λ)=0得λ=1.
又S(1)=2,S =
=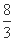 ,S(2)=
,S(2)= 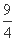 ,
,
∴当λ=1时,△AOB的面积取得最小值2,当λ=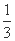 时,
时,
△AOB的面积取得最大值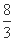 .
.
∴△AOB面积的取值范围是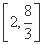 .
.


科目:高中数学 来源: 题型:
已知函数f(x)=(x-a)2(x-b)(a,b∈R,a<b).
(1)当a=1,b=2时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)设x1,x2是f(x)的两个极值点,x3是f(x)的一个零点,且x3≠x1,x3≠x2.证明:存在实数x4,使得x1,x2,x3,x4按某种顺序排列后构成等差数列,并求x4.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知F1、F2为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则|PF1|·|PF2|=( )
(A)2 (B)4 (C)6 (D)8
查看答案和解析>>
科目:高中数学 来源: 题型:
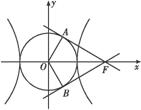
过双曲线C: 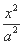 -
-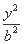 =1(a>0,b>0)的一个焦点作圆x2+y2=a2的两条切线,切点分别为A、B.若∠AOB=120°(O是坐标原点),则双曲线C的离心率为 .
=1(a>0,b>0)的一个焦点作圆x2+y2=a2的两条切线,切点分别为A、B.若∠AOB=120°(O是坐标原点),则双曲线C的离心率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线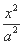 -
-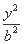 =1(a>0,b>0),过其右焦点F且垂直于实轴的直线与双曲线交于M,N两点,O为坐标原点.若OM⊥ON,则双曲线的离心率为( )
=1(a>0,b>0),过其右焦点F且垂直于实轴的直线与双曲线交于M,N两点,O为坐标原点.若OM⊥ON,则双曲线的离心率为( )
(A)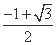 (B)
(B)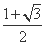
(C)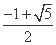 (D)
(D)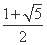
查看答案和解析>>
科目:高中数学 来源: 题型:
已知F1,F2为双曲线Ax2-By2=1的焦点,其顶点是线段F1F2的三等分点,则其渐近线的方程为( )
(A)y=±2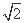 x (B)y=±
x (B)y=± x
x
(C)y=±x (D)y=±2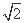 x或y=±
x或y=± x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线 -
- =1(a>0,b>0)的一条渐近线方程是y=
=1(a>0,b>0)的一条渐近线方程是y= x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
(A) 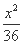 -
- 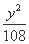 =1 (B)
=1 (B)  -
-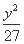 =1
=1
(C) 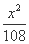 -
-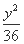 =1 (D)
=1 (D) 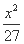 -
-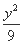 =1
=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com