
已知双曲线 -
- =1(a>0,b>0)的一条渐近线方程是y=
=1(a>0,b>0)的一条渐近线方程是y= x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
(A) 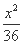 -
- 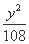 =1 (B)
=1 (B)  -
-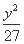 =1
=1
(C) 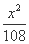 -
-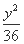 =1 (D)
=1 (D) 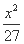 -
-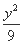 =1
=1
 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
直线与双曲线位置关系的判定及应用
已知双曲线C的方程为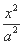 -
-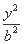 =1(a>0,b>0),离心率e=
=1(a>0,b>0),离心率e=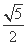 ,顶点到渐近线的距离为
,顶点到渐近线的距离为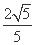 .
.
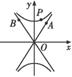
(1)求双曲线C的方程;
(2)如图,P是双曲线C上一点,A、B两点在双曲线C的两条渐近线上,且分别位于第一、二象限.
若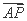 =λ
=λ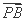 ,λ∈
,λ∈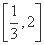 .求△AOB的面积的取值范围.
.求△AOB的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C1:  +
+ =1(a>b>0)与双曲线C2:x2-
=1(a>b>0)与双曲线C2:x2-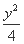 =1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
(A)a2=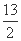 (B)a2=13
(B)a2=13
(C)b2= (D)b2=2
(D)b2=2
查看答案和解析>>
科目:高中数学 来源: 题型:
抛物线C1:y= x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2:  -y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p等于( )
-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p等于( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,已知圆P在x轴上截得线段长为2 ,在y轴上截得线段长为2
,在y轴上截得线段长为2 .
.
(1)求圆心P的轨迹方程;
(2)若P点到直线y=x的距离为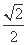 ,求圆P的方程.
,求圆P的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
点A为两曲线C1:  +
+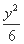 =1和C2:x2-
=1和C2:x2-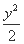 =1在第二象限的交点,B、C为曲线C1的左、右焦点,线段BC上一点P满足:
=1在第二象限的交点,B、C为曲线C1的左、右焦点,线段BC上一点P满足:  =
= +m(
+m( +
+ ),则实数m的值为 .
),则实数m的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
当前,某城市正分批修建经济适用房以解决低收入家庭住房紧张问题.已知甲、乙、丙三个社区现分别有低收入家庭360户、270户、180户,若第一批经济适用房中有90套住房用于解决这三个社区中90户低收入家庭的住房问题,现采用分层抽样的方法决定各社区户数,则应从乙社区中抽取低收入家庭的户数为( )
A.40 B.36 C.30 D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com