
当前,某城市正分批修建经济适用房以解决低收入家庭住房紧张问题.已知甲、乙、丙三个社区现分别有低收入家庭360户、270户、180户,若第一批经济适用房中有90套住房用于解决这三个社区中90户低收入家庭的住房问题,现采用分层抽样的方法决定各社区户数,则应从乙社区中抽取低收入家庭的户数为( )
A.40 B.36 C.30 D.20
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
已知双曲线 -
- =1(a>0,b>0)的一条渐近线方程是y=
=1(a>0,b>0)的一条渐近线方程是y= x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
(A) 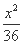 -
- 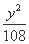 =1 (B)
=1 (B)  -
-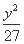 =1
=1
(C) 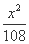 -
-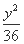 =1 (D)
=1 (D) 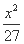 -
-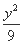 =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
过双曲线 -
- =1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若T为线段FP的中点,则该双曲线的渐近线方程为( )
=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若T为线段FP的中点,则该双曲线的渐近线方程为( )
(A)x±y=0 (B)2x±y=0
(C)4x±y=0 (D)x±2y=0
查看答案和解析>>
科目:高中数学 来源: 题型:
已知A,B分别是椭圆C1:  +
+ =1的左、右顶点,P是椭圆上异于A,B的任意一点,Q是双曲线C2:
=1的左、右顶点,P是椭圆上异于A,B的任意一点,Q是双曲线C2:  -
-  =1上异于A,B的任意一点,a>b>0.
=1上异于A,B的任意一点,a>b>0.
(1)若P(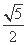 ,
, ),Q(
),Q( ,1),求椭圆C1的方程;
,1),求椭圆C1的方程;
(2)记直线AP,BP,AQ,BQ的斜率分别是k1,k2,k3,k4,求证:k1·k2+k3·k4为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
一个总体中的80个个体编号为0,1,2,…,79,并依次将其分为8个组,组号为0,1,…,7,要用(错位)系统抽样的方法抽取一个容量为8的样本.即规定先在第0组随机抽取一个号码,记为i,依次错位地得到后面各组的号码,即第k组中抽取个位数字为i+k(当i+k<10)或i+k-10(当i+k≥10)的号码.在i=6时,所抽到的8个号码是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程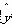 =3-5x,变量x增加一个单位时,y平均增加5个单位;
=3-5x,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程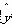 =
=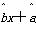 必过点(
必过点(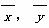 );
);
④在一个2×2列联表中,由计算得K2=13.079,则有99%的把握确认这两个变量间有关系.
其中错误的个数是( )
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com