练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知A,B分别是椭圆C1: +=1的左、右顶点,P是椭圆上异于A,B的任意一点,Q是双曲线C2: - =1上异于A,B的任意一点,a>b>0.

    (1)若P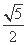（,）,Q（,1）,求椭圆C1的方程;

    (2)记直线AP,BP,AQ,BQ的斜率分别是k1,k2,k3,k4,求证:k1·k2+k3·k4为定值.


     (1)解:由解得

    ∴椭圆C1的方程为+=1.

    (2)证明:由题意知A(-a,0),B(a,0),

    设P(x1,y1),(x1≠±a)则+=1,

    ∴=b2（1-）=(a2-).

    设Q(x2,y2),(x2≠±a),则-=1,

    ∴=b2（-1）=(-a2).

    ∴k1=,k2=,k3=,k3=.

    ∴k1·k2+k3·k4=+

    =+

    =0.

    即k1k2+k3k4为定值,定值是0.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设椭圆C: +=1(a>b>0)的左、右焦点分别为F1,F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为(　　)

    (A)        (B)         (C)  (D)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    抛物线C1:y=x2(p>0)的焦点与双曲线C2: -y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p等于(　　)

    (A) (B) (C)    (D)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    点A为两曲线C1: +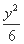=1和C2:x2-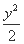=1在第二象限的交点,B、C为曲线C1的左、右焦点,线段BC上一点P满足: =+m(+),则实数m的值为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的右侧),且|MN|=3,已知椭圆D: +=1(a>b>0)的焦距等于2|ON|,且过点（,）.

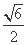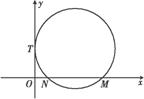
    (1)求圆C和椭圆D的方程;

    (2)若过点M斜率不为零的直线l与椭圆D交于A、B两点,求证:直线NA与直线NB的倾斜角互补.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    当前，某城市正分批修建经济适用房以解决低收入家庭住房紧张问题．已知甲、乙、丙三个社区现分别有低收入家庭360户、270户、180户，若第一批经济适用房中有90套住房用于解决这三个社区中90户低收入家庭的住房问题，现采用分层抽样的方法决定各社区户数，则应从乙社区中抽取低收入家庭的户数为(　　)

    A．40  B．36  C．30  D．20

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某单位有工程师6人，技术员12人，技工18人，要从这些人中抽取一个容量为n的样本．如果采用系统抽样法和分层抽样法抽取，不用剔除个体；如果样本容量增加一个，则在采用系统抽样时，需要在总体中先剔除1个个体．求样本容量n.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    两个变量y与x的回归模型中，分别选择了4个不同模型，计算出它们的相关指数R2如下，其中拟合效果最好的模型是(　　)

    A．模型1(相关指数R2为0.97)

    B．模型2(相关指数R2为0.89)

    C．模型3(相关指数R2为0.56)

    D．模型4(相关指数R2为0.45)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合M＝{x|－2≤x≤8}，N＝{x|x2－3x＋2≤0}，在集合M中任取一个元素x，则“x∈M∩N”的概率是(　　)

    A.  B.  C.  D.

    查看答案和解析>>

    同步练习册答案