练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    下列说法：

    ①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变；

    ②设有一个回归方程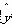＝3－5x，变量x增加一个单位时，y平均增加5个单位；

    ③线性回归方程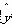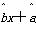＝必过点()；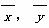

    ④在一个2×2列联表中，由计算得K2＝13.079，则有99%的把握确认这两个变量间有关系．

    其中错误的个数是(　　)

    A．0  B．1  C．2  D．3


    B


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


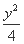    已知椭圆C1: +=1(a>b>0)与双曲线C2:x2-=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则(　　)

    (A)a2=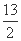   (B)a2=13

    (C)b2=    (D)b2=2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    当前，某城市正分批修建经济适用房以解决低收入家庭住房紧张问题．已知甲、乙、丙三个社区现分别有低收入家庭360户、270户、180户，若第一批经济适用房中有90套住房用于解决这三个社区中90户低收入家庭的住房问题，现采用分层抽样的方法决定各社区户数，则应从乙社区中抽取低收入家庭的户数为(　　)

    A．40  B．36  C．30  D．20

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知总体的各个个体的值由小到大依次为3,7，a，b,12,20，且总体的中位数为12，若要使该总体的标准差最小，则a＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    两个变量y与x的回归模型中，分别选择了4个不同模型，计算出它们的相关指数R2如下，其中拟合效果最好的模型是(　　)

    A．模型1(相关指数R2为0.97)

    B．模型2(相关指数R2为0.89)

    C．模型3(相关指数R2为0.56)

    D．模型4(相关指数R2为0.45)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某工厂用甲、乙两种不同工艺生产一大批同一种零件，零件尺寸均在[21.7,22.3](单位：cm)之间，把零件尺寸在[21.9,22.1)的记为一等品，尺寸在[21.8,21.9)∪[22.1,22.2)的记为二等品，尺寸在[21.7,21.8)∪[22.2,22.3]的记为三等品，现从甲、乙工艺生产的零件中各随机抽取100件产品，所得零件尺寸的频率分布直方图如图所示：

    根据上述数据完成下列2×2列联表，根据此数据你认为选择不同的工艺与生产出一等品是否有关？

     

    甲工艺

    乙工艺

    合计

    一等品

    非一等品

    合计

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若A、B为互斥事件，P(A)＝0.4，P(A∪B)＝0.7，则P(B)＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某市为了了解今年高中毕业生的体能状况，从本市某校高中毕业班中抽取一个班进行铅球测试，成绩在8.0米(精确到0.1米)以上的为合格．把所得数据进行整理后，分成6组画出频率分布直方图的一部分(如图)，已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.

    (1)求这次铅球测试成绩合格的人数；

    (2)若由直方图来估计这组数据的中位数，指出它在第几组内，并说明理由；

    (3)若参加此次测试的学生中，有9人的成绩为优秀，现在要从成绩优秀的学生中，随机选出2人参加“毕业运动会”，已知a、b的成绩均为优秀，求两人至少有1人入选的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    甲、乙、丙三人站成一排，其中甲、乙两人不排在一起的概率为________．

    查看答案和解析>>

    同步练习册答案