
在平面直角坐标系xOy中,已知圆P在x轴上截得线段长为2 ,在y轴上截得线段长为2
,在y轴上截得线段长为2 .
.
(1)求圆心P的轨迹方程;
(2)若P点到直线y=x的距离为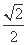 ,求圆P的方程.
,求圆P的方程.
科目:高中数学 来源: 题型:
已知双曲线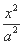 -
-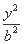 =1(a>0,b>0),过其右焦点F且垂直于实轴的直线与双曲线交于M,N两点,O为坐标原点.若OM⊥ON,则双曲线的离心率为( )
=1(a>0,b>0),过其右焦点F且垂直于实轴的直线与双曲线交于M,N两点,O为坐标原点.若OM⊥ON,则双曲线的离心率为( )
(A)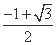 (B)
(B)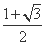
(C)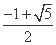 (D)
(D)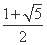
查看答案和解析>>
科目:高中数学 来源: 题型:
椭圆E:  +
+ =1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.
(1)求椭圆E的方程;
(2)若过F1的直线l交椭圆于A,B两点,判断是否存在直线l使得∠AF2B为钝角,若存在,求出l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,已知抛物线C1:x2+by=b2经过椭圆C2:  +
+ =1(a>b>0)的两个焦点.
=1(a>b>0)的两个焦点.
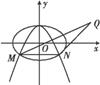
(1)求椭圆C2的离心率;
(2)设点Q(3,b),又M,N为C1与C2不在y轴上的两个交点,若△QMN的重心在抛物线C1上,求C1和C2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线 -
- =1(a>0,b>0)的一条渐近线方程是y=
=1(a>0,b>0)的一条渐近线方程是y= x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
(A) 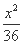 -
- 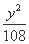 =1 (B)
=1 (B)  -
-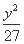 =1
=1
(C) 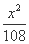 -
-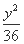 =1 (D)
=1 (D) 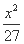 -
-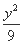 =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,已知抛物线E:y2=x与圆M:(x-4)2+y2=r2(r>0)相交于A、B、C、D四个点.
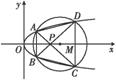
(1)求r的取值范围;
(2)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
过双曲线 -
- =1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若T为线段FP的中点,则该双曲线的渐近线方程为( )
=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若T为线段FP的中点,则该双曲线的渐近线方程为( )
(A)x±y=0 (B)2x±y=0
(C)4x±y=0 (D)x±2y=0
查看答案和解析>>
科目:高中数学 来源: 题型:
一个总体中的80个个体编号为0,1,2,…,79,并依次将其分为8个组,组号为0,1,…,7,要用(错位)系统抽样的方法抽取一个容量为8的样本.即规定先在第0组随机抽取一个号码,记为i,依次错位地得到后面各组的号码,即第k组中抽取个位数字为i+k(当i+k<10)或i+k-10(当i+k≥10)的号码.在i=6时,所抽到的8个号码是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130 t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
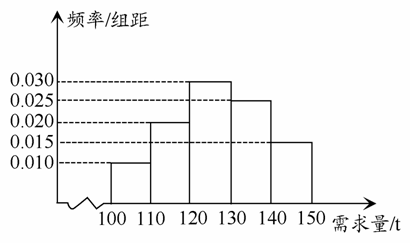
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com