
 如图,在四面体P-ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC=$\frac{2\sqrt{3}}{3}$.
如图,在四面体P-ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC=$\frac{2\sqrt{3}}{3}$.分析 (1)连接AC交BD于O,利用线线垂直得到线面垂直,即可证明PA⊥BD;
(2)当E为PA的中点时,BE∥平面PCD,并证明,并得到点E到平面ABCD的距离等于$\frac{1}{2}$PC,问题得以解决.
解答 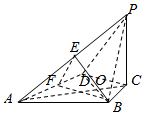 解:(1)证明:连接AC交BD于O,
解:(1)证明:连接AC交BD于O,
∵PC⊥BP,BP∩CP=P,
∴PC⊥AB,
∵AB⊥BP,BP∩CP=P,
∴AB⊥平面PBC,
∴AB⊥BC,
∵BC=$\frac{2\sqrt{3}}{3}$,
∴tan∠BAC=$\frac{\sqrt{3}}{3}$,即∠BAC=30°,
∵∠ABD=60°,
∴∠AOB=90°,
∴AC⊥BD,
∵PC⊥BD,
∴BD⊥平面ACP,
∵AP?平面APC,
∴PA⊥BD,
(2)取AD的中点F,连接BF,EF,
当E为PA的中点时,BE∥平面PCD,证明如下,
∵AB=BD,
∴BF⊥AD,
有(1)的BC=CD,则CD⊥AD,
∴EF∥CD,
∵E为PA的中点,
∴EF∥PD,
∴平面BEF∥平面PCD,
∵BE?平面BEF,
∴BE∥平面PCD,
∵PC⊥底面ABCD,
∴点E到平面ABCD的距离等于$\frac{1}{2}$PC=1
点评 本题考查直线 与平面垂直的判定,直线与直线平行,考查空间想象能力,逻辑思维能力,是中档题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{22}{7}$ | B. | $\frac{63}{20}$ | C. | $\frac{78}{25}$ | D. | $\frac{109}{35}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | a>c>b | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{{3\sqrt{5}}}{2}$ | B. | $3\sqrt{6}$ | C. | $2\sqrt{3}$ | D. | $\frac{{5\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD是矩形,AB=4,BC=2$\sqrt{3}$,四边形CDEF是菱形,∠DEF=60°,且平面CDEF⊥平面ABCD,M,N分别是线段EF,CD上的点,满足EM=3MF.CN=3ND,AC与BN交于点P.
如图,四边形ABCD是矩形,AB=4,BC=2$\sqrt{3}$,四边形CDEF是菱形,∠DEF=60°,且平面CDEF⊥平面ABCD,M,N分别是线段EF,CD上的点,满足EM=3MF.CN=3ND,AC与BN交于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | [3,+∞) | C. | (-∞,2] | D. | (-∞,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为1,$\widehat{CE}$所对的圆心角∠CDE=90°,将图形ABCE绕AE所在直线旋转一周,形成的几何体的表面积为5π.
如图,正方形ABCD的边长为1,$\widehat{CE}$所对的圆心角∠CDE=90°,将图形ABCE绕AE所在直线旋转一周,形成的几何体的表面积为5π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com