
 如图,正方形ABCD的边长为1,$\widehat{CE}$所对的圆心角∠CDE=90°,将图形ABCE绕AE所在直线旋转一周,形成的几何体的表面积为5π.
如图,正方形ABCD的边长为1,$\widehat{CE}$所对的圆心角∠CDE=90°,将图形ABCE绕AE所在直线旋转一周,形成的几何体的表面积为5π.  手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:选择题
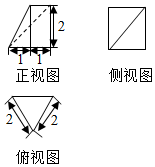 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四面体P-ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC=$\frac{2\sqrt{3}}{3}$.
如图,在四面体P-ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC=$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{5}{2}$] | B. | (-∞,$\frac{1}{2}$]∪(1,$\frac{5}{2}$] | C. | [$\frac{1}{2}$,$\frac{5}{2}$) | D. | [$\frac{1}{2}$,1)∪[$\frac{5}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
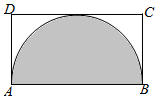 如图所示,在矩形ABCD中,AB=2a,AD=a,图中阴影部分是以AB为直径的半圆,现在向矩形ABCD内随机撒4000粒豆子(豆子的大小忽略不计),根据你所学的概率统计知识,下列四个选项中最有可能落在阴影部分内的豆子数目是( )
如图所示,在矩形ABCD中,AB=2a,AD=a,图中阴影部分是以AB为直径的半圆,现在向矩形ABCD内随机撒4000粒豆子(豆子的大小忽略不计),根据你所学的概率统计知识,下列四个选项中最有可能落在阴影部分内的豆子数目是( )| A. | 1000π | B. | 2000π | C. | 3000π | D. | 400π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 28 | C. | 30 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在等差数列{an}中,若ap+aq=ar+aδ,则p+q=r+δ | |
| B. | 已知数列{an}的前n项和为Sn,若{an}是等比数列,则Sk,S2k-Sk,S3k-S2k也是等比数列 | |
| C. | 在数列{an}中,若ap+aq=2ar,则ap,ar,aq成等差数列 | |
| D. | 在数列{an}中,若ap•aq=a${\;}_{r}^{2}$,则ap,ar,aq成等比数列 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com