
| A. | (1,$\frac{5}{2}$] | B. | (-∞,$\frac{1}{2}$]∪(1,$\frac{5}{2}$] | C. | [$\frac{1}{2}$,$\frac{5}{2}$) | D. | [$\frac{1}{2}$,1)∪[$\frac{5}{2}$,+∞) |
分析 当p为真命题时,根据对数型函数单调性的规律得到0<a<1;根据一元二次方程根的判别式,得到当q为真命题时,0<a<$\frac{1}{2}$或a>$\frac{5}{2}$,因为“P∨Q”为假,说明命题p、q都为假,可得a的取值范围.
解答 解:先看命题p:
∵函数y=loga(x+1)在(0,+∞)内单调递减,a>0,a≠1,
∴命题P为真时?0<a<1,
再看命题q:
当命题q为真时,二次函数对应的一元二次方程根的判别式满足:
△=(2a-3)2-4>0⇒0<a<$\frac{1}{2}$或a>$\frac{5}{2}$,
由“p∨q”为假,知p、q都为假,
∴$\left\{\begin{array}{l}{a>1}\\{\frac{1}{2}≤a≤\frac{5}{2}}\end{array}\right.$,解得:1<a≤$\frac{5}{2}$
故选:A.
点评 本题以函数的单调性和二次函数零点的问题为载体,考查了命题真假的判断与应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
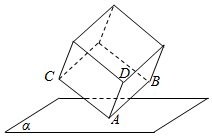 如图,棱长为3的正方体的顶点A在平面α上,三条棱AB,AC,AD都在平面α的同侧,若顶点B,C到平面α的距离分别为1,$\sqrt{2}$,则顶点D到平面α的距离是$\sqrt{6}$.
如图,棱长为3的正方体的顶点A在平面α上,三条棱AB,AC,AD都在平面α的同侧,若顶点B,C到平面α的距离分别为1,$\sqrt{2}$,则顶点D到平面α的距离是$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD是矩形,AB=4,BC=2$\sqrt{3}$,四边形CDEF是菱形,∠DEF=60°,且平面CDEF⊥平面ABCD,M,N分别是线段EF,CD上的点,满足EM=3MF.CN=3ND,AC与BN交于点P.
如图,四边形ABCD是矩形,AB=4,BC=2$\sqrt{3}$,四边形CDEF是菱形,∠DEF=60°,且平面CDEF⊥平面ABCD,M,N分别是线段EF,CD上的点,满足EM=3MF.CN=3ND,AC与BN交于点P.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为1,$\widehat{CE}$所对的圆心角∠CDE=90°,将图形ABCE绕AE所在直线旋转一周,形成的几何体的表面积为5π.
如图,正方形ABCD的边长为1,$\widehat{CE}$所对的圆心角∠CDE=90°,将图形ABCE绕AE所在直线旋转一周,形成的几何体的表面积为5π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
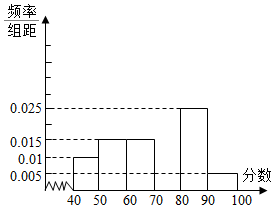 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
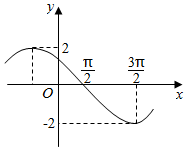 已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),函数f(x)的图象如图所示,则f(0)的值为( )
已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),函数f(x)的图象如图所示,则f(0)的值为( )| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b≥2$\sqrt{ab}$ | B. | a2+b2>2ab | C. | $\frac{a}{b}$+$\frac{b}{a}$≥2 | D. | |${\frac{a}{b}$+$\frac{b}{a}}$|≥2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com