
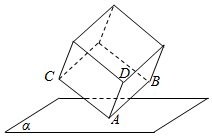
 如图,棱长为3的正方体的顶点A在平面α上,三条棱AB,AC,AD都在平面α的同侧,若顶点B,C到平面α的距离分别为1,$\sqrt{2}$,则顶点D到平面α的距离是$\sqrt{6}$.
如图,棱长为3的正方体的顶点A在平面α上,三条棱AB,AC,AD都在平面α的同侧,若顶点B,C到平面α的距离分别为1,$\sqrt{2}$,则顶点D到平面α的距离是$\sqrt{6}$. 分析 本题的条件正规,但位置不正规.牵涉到的知识虽然只有线面距离和线面角,但难于下手.出路何在?在正方体的8个顶点中,有关系的只有4个(其他顶点可不予理会).这4点组成直角四面体,这就是本题的根.所以最终归结为:已知直角四面体的3个顶点A,B,C到平面M的距离依次为0,1,$\sqrt{2}$,求顶点D到平面M的距离.
解答  解:如图,连结BC、CD、BD,则四面体A-BCD为直角四面体.作平面M的法线AH,再作,BB1⊥平面M于B1,CC1⊥平面M于C1,DD1⊥平面M于D1.
解:如图,连结BC、CD、BD,则四面体A-BCD为直角四面体.作平面M的法线AH,再作,BB1⊥平面M于B1,CC1⊥平面M于C1,DD1⊥平面M于D1.
连结AB1,AC1,AD1,令AH=h,DA=a,DB=b,DC=c,
由等体积可得$\frac{1}{{h}^{2}}$=$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$+$\frac{1}{{c}^{2}}$,
∴$\frac{{h}^{2}}{{a}^{2}}$+$\frac{{h}^{2}}{{b}^{2}}$+$\frac{{h}^{2}}{{c}^{2}}$=1
令∠BAB1=α,∠CAC1=β,∠DAD1=γ,
可得sin2α+sin2β+sin2γ=1,
设DD1=m,∵BB1=1,CC1=$\sqrt{2}$,
∴$(\frac{1}{3})^{2}+(\frac{\sqrt{2}}{3})^{2}+(\frac{m}{3})^{2}$=1
解得m=$\sqrt{6}$.即所求点D到平面α的距离为$\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 本题考查点D到平面α的距离,考查线面角,考查学生分析解决问题的能力,难度大.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $8\sqrt{2}$ | B. | 46 | C. | $2\sqrt{23}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
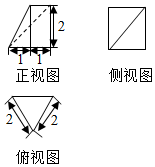 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
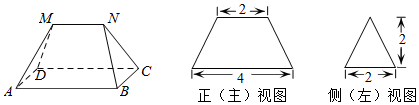
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{5}{2}$] | B. | (-∞,$\frac{1}{2}$]∪(1,$\frac{5}{2}$] | C. | [$\frac{1}{2}$,$\frac{5}{2}$) | D. | [$\frac{1}{2}$,1)∪[$\frac{5}{2}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com