
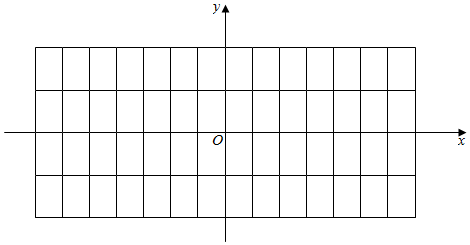
分析 (1)根据五点法作图的方法先取值,然后描点即可得到图象.
(2)根据函数的对称性以及函数的单调性即可得到结论.
(3)根据函数最值的性质解方程即可.
解答 解:(1)列表:
| x | -$\frac{π}{8}$ | $\frac{π}{8}$ | $\frac{3π}{8}$ | $\frac{5π}{8}$ | $\frac{7π}{8}$ |
| 2x+$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| y | 0 | 1 | 0 | -1 | 0 |

点评 本题主要考查三角函数的图象的作法,考查了正弦函数的对称性,单调性,利用五点法是解决三角函数图象的基本方法.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
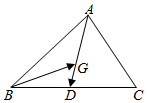 如图,在△ABC中,点D是边BC的中点,点G在AD上,且是△ABC的重心,则用向量$\overrightarrow{AB},\overrightarrow{AC}$表示$\overrightarrow{BG}$为( )
如图,在△ABC中,点D是边BC的中点,点G在AD上,且是△ABC的重心,则用向量$\overrightarrow{AB},\overrightarrow{AC}$表示$\overrightarrow{BG}$为( )| A. | $\overrightarrow{BG}=-\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | B. | $\overrightarrow{BG}=-\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$ | C. | $\overrightarrow{BG}=\frac{2}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AC}$ | D. | $\overrightarrow{BG}=\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [1,2] | C. | [1,$\frac{3}{2}$] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -2$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50,0.15 | B. | 50,0.75 | C. | 100,0.15 | D. | 100,0.75 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a13 | B. | a15 | C. | a10和a11 | D. | a16和a17 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
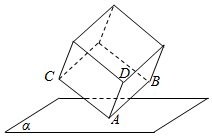 如图,棱长为3的正方体的顶点A在平面α上,三条棱AB,AC,AD都在平面α的同侧,若顶点B,C到平面α的距离分别为1,$\sqrt{2}$,则顶点D到平面α的距离是$\sqrt{6}$.
如图,棱长为3的正方体的顶点A在平面α上,三条棱AB,AC,AD都在平面α的同侧,若顶点B,C到平面α的距离分别为1,$\sqrt{2}$,则顶点D到平面α的距离是$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com