若向量$\overrightarrow{a}$=(4.3).$\overrightarrow{b}$=.则$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为( )A．-2B．2C．-2$\sqrt{2}$D．2$\sqrt{2}$ 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

12．若向量$\overrightarrow{a}$=（4，3），$\overrightarrow{b}$=（-1，-2），则$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为（　　）

A．

-2

B．

C．

-2$\sqrt{2}$

D．

2$\sqrt{2}$

分析根据投影的定义即可求出．

解答解：∵向量$\overrightarrow{a}$=（4，3），$\overrightarrow{b}$=（-1，-2），
∴$\overrightarrow{a}•\overrightarrow{b}$=4×（-1）+3×（-2）=-10，|$\overrightarrow{a}$|=$\sqrt{{4}^{2}+{3}^{2}}$=5
∴$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$=$\frac{-10}{5}$=-2，
故选：A．

点评本题考查向量的投影的求解，化为数量积来求是解决问题的关键，属基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

2．（x-y）²（x+y）⁷的展开式中x³y⁶的系数为0（用数字作答）

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

3．

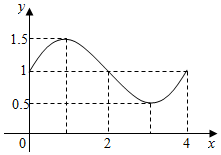函数f（x）=Asin（ωx+φ）+b的图象如图，则f（x）的解析式和S=f（1）+f（2）+f（3）+…+f（2013）+f（2014）+f（2015）+f（2016）的值分别为（　　）

	A．	f（x）=$\frac{1}{2}$sin$\frac{π}{2}$x+1，S=2016		B．	f（x）=$\frac{1}{2}$cos$\frac{π}{2}$x+1，S=2016
	C．	f（x）=$\frac{1}{2}$sin$\frac{π}{2}$x+1，S=2016.5		D．	f（x）=$\frac{1}{2}$cos$\frac{π}{2}$x+1，S=2016.5

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

20．某市汽车牌照号码构成是：前两位为英文字母，后三位数字，如DE668，其中牌照号码最后一个数字为8的牌照号码共有（　　）

A．

（C${\;}_{26}^{1}$）²A${\;}_{10}^{2}$

B．

A${\;}_{26}^{2}$A${\;}_{10}^{2}$

C．

（C${\;}_{26}^{1}$）²10²

D．

A${\;}_{26}^{2}$10²

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

7．某班一次数学测试成绩的茎叶图（茎上数代表十位，叶上数代表个位）如图1所示．
（1）以10为组距，在图2给定的坐标系中画出该班成绩的频率分布直方图；
（2）用分层抽样的方法抽取一个容量为8的样本，在样本中从分数在[60，80）之间的试卷中任取3份分析学生失分情况，设抽取的试卷分数在[70，80）的分数为X，求X的分布列和数学期望．