
分析 (1)记A0表示事件“取出的2件产品中没有二等品”,A1表示事件“取出的2件产品中恰有1件二等品”,则A1与A0互斥,且A=A0+A1,由此能求出事件A:“取出的2件产品中至多有1件是二等品”的概率.
(2)随机变量X的所有可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答 解:(1)记A0表示事件“取出的2件产品中没有二等品”,
A1表示事件“取出的2件产品中恰有1件二等品”,
则A1与A0互斥,且A=A0+A1,
∴P(A)=P(A0)+P(A1)=(1-0.2)2+C${\;}_{2}^{1}$×0.2×(1-0.2)=0.96.
(2)随机变量X的所有可能取值为0,1,2,
该产品共有二等品20×0.2=4(件),
P(X=0)=$\frac{{C}_{16}^{2}}{{C}_{20}^{2}}$=$\frac{12}{19}$,
P(X=1)=$\frac{{C}_{16}^{1}{C}_{4}^{1}}{{C}_{20}^{2}}$=$\frac{32}{90}$,
P(X=2)=$\frac{{C}_{4}^{3}}{{C}_{20}^{2}}$=$\frac{3}{93}$,
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{12}{19}$ | $\frac{32}{95}$ | $\frac{3}{95}$ |
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意互斥事件概率加法公式和排列组合知识的合理运用.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:选择题

| A. | $\frac{5}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
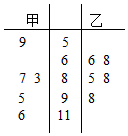 雾霾天气是一种大气污染状态,PM2.5被认为是造成雾霾天气的“元凶”,PM2.5日均值越小,空气质量越好.国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如表:
雾霾天气是一种大气污染状态,PM2.5被认为是造成雾霾天气的“元凶”,PM2.5日均值越小,空气质量越好.国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如表:| PM2.5日均值 (微克/立方米) | 0--35 | 35--75 | 75--115 | 115--150 | 150--250 | 250以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级 轻度污染 | 4级 中度污染 | 5级 重度污染 | 6级 严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x≤1} | B. | {x|-1≤x<1} | C. | {x|-1≤x≤1} | D. | {x|-1<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com