Question

12．雾霾天气是一种大气污染状态，PM2.5被认为是造成雾霾天气的“元凶”，PM2.5日均值越小，空气质量越好．国家环境标准设定的PM2.5日均值（微克/立方米）与空气质量等级对应关系如表：

PM2.5日均值 （微克/立方米）	0--35	35--75	75--115	115--150	150--250	250以上
空气质量等级	1级优	2级良	3级 轻度污染	4级 中度污染	5级 重度污染	6级 严重污染

由某市城市环境监测网获得4月份某5天甲、乙两城市的空气质量指数数据，用茎叶图表示，如图所示．
（Ⅰ）试根据统计数据，分别写出两城区的PM2.5日均值的中位数，并从中位数角度判断哪个城区的空气质量较好？
（Ⅱ）考虑用频率估计概率的方法，试根据统计数据，估计甲城区某一天空气质量等级为3级轻度污染的概率；
（Ⅲ）分别从甲、乙两个城区的统计数据中任取一个，试求这两城区空气质量等级相同的概率．

Answer 1

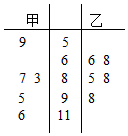
分析 （I）由茎叶图可知甲乙两个城市5天数据由小到大排列，求出中位数，比较两个中位数的大小可得哪个城市的空气质量较好；
（II）由茎叶图可知在抽取的五天中，甲城市空气质量等级为3级轻度污染的频数为3，进而得到频率，进而估算出概率；
（Ⅲ）从甲城市和乙城市的统计数据中任取一个，共有25种不同情况，统计这两个城市空气质量等级相同的情况个数，代入古典概型概率计算公式可得答案．

解答 解：（Ⅰ）甲城市5天数据由小到大排列：
59，83，87，95，116，
乙城市5天数据由小到大排列：
66，68，85，88，98，
∴甲的中位数是87，乙的中位数是85，
∴乙城市的空气质量较好．
（Ⅱ）根据上面的统计数据，可得在这五天中甲城市空气质量等级为3级轻度污染的频率为$\frac{3}{5}$，
则估计甲城市某一天的空气质量等级为3级轻度污染的概率为$\frac{3}{5}$．        
（Ⅲ）设事件A：从甲城市和乙城市的上述数据中分别任取一个，这两个城市的空气质量等级相同，
由题意可知，从甲城市和乙城市的监测数据中分别任取一个，共有25个结果，分别记为：
（59，66），（59，68），（59，85），（59，88）（59，98）
（83，66），（83，68），（83，85），（83，88）（83，98）
（87，66），（87，68），（87，85），（87，88）（87，98）
（95，66），（95，68），（95，85），（95，88）（95，98）
（116，66），（116，68），（116，85），（116，88）（116，98），
其数据表示两城市空气质量等级相同的包括同为2级良的为甲59，乙66，乙68；
同为3级轻度污染的为甲83，甲87，甲95； 乙85，乙88，乙98；则空气质量等级相同的为：
（59，66），（59，68），
（83，85），（83，88），（83，98），
（87，85），（87，88），（87，98），
（95，85），（95，88），（95，98），
共11个结果．
所以这两个城市空气质量等级相同的概率为$\frac{11}{25}$．

点评 本题考查等可能事件概率的求法，考查茎叶图，考查利用数学知识解决实际问题，属于基础题．