
| 年级 | 相关人数 | 抽取人数 |
| 高一 | 36 | x |
| 高二 | 54 | 3 |
| 高三 | 18 | y |
分析 (Ⅰ)根据分层抽样,抽取人数与相关人员数对应成比例的原则,结合已知中高中三个年级的相关人员数及从高三年级中抽取的人数,易求得x,y的值.
(Ⅱ)设从高二年级抽取的3人为A,B,C,从高三年级抽取的1人为a,从中随机选2人,我们用列举法列出所有不同的选取结果的个数,及满足条件选中的2人都来自高二的结果个数,即可得到答案.
解答 解:(Ⅰ)x=36×$\frac{3}{54}$=2,y=18×$\frac{3}{54}$=1;
(Ⅱ)记从高二年级抽取的3人为A,B,C,从高三年级抽取的1人为a,
则从这两个年级中抽取的4人中选2人的基本事件有:
(A,B),(A,C),(B,C),(A,a),
(B,a),(C,a),共6种.
设选中的2人都来自高二的事件为A,
共(A,B),(A,C),(B,C)3种,
故P(A)=$\frac{3}{6}$=$\frac{1}{2}$.
点评 本题考查的知识点是古典概型,及分层抽样,其中用列举法计算基本事件数及事件性质的概率是古典概型最常用的方法.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 雾霾天气是一种大气污染状态,PM2.5被认为是造成雾霾天气的“元凶”,PM2.5日均值越小,空气质量越好.国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如表:
雾霾天气是一种大气污染状态,PM2.5被认为是造成雾霾天气的“元凶”,PM2.5日均值越小,空气质量越好.国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如表:| PM2.5日均值 (微克/立方米) | 0--35 | 35--75 | 75--115 | 115--150 | 150--250 | 250以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级 轻度污染 | 4级 中度污染 | 5级 重度污染 | 6级 严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 14 | C. | 13 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x≤1} | B. | {x|-1≤x<1} | C. | {x|-1≤x≤1} | D. | {x|-1<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
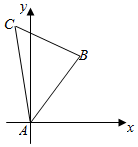 在平面直角坐标系中,两点P1(x1,y1),P2(x2,y2)间的“L-距离”定义为|P1P2|=|x1-x2|+|y1-y2|.现将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的斜率为k,0≤k≤$\sqrt{3}$.求:当|BC|取最大值时,边AB所在直线的斜率的值.
在平面直角坐标系中,两点P1(x1,y1),P2(x2,y2)间的“L-距离”定义为|P1P2|=|x1-x2|+|y1-y2|.现将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的斜率为k,0≤k≤$\sqrt{3}$.求:当|BC|取最大值时,边AB所在直线的斜率的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com