将序号分别为1.2.3.4.5的5张参观券全部分给4人.每人至少1张．如果分给同一人的2张参观券连号.那么不同的分法种数是( )A．24B．96C．144D．210 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

20．将序号分别为1，2，3，4，5的5张参观券全部分给4人，每人至少1张．如果分给同一人的2张参观券连号，那么不同的分法种数是（　　）

A．

B．

C．

144

D．

210

分析求出5张参观券全部分给4人，每人至少1张，如果分给同一人的2张参观券连号的组数，然后分给4人排列即可．

解答解：5张参观券全部分给4人，分给同一人的2张参观券连号，
方法数为：1和2，2和3，3和4，4和5，四种连号，其它号码各为一组，分给4人，共有4×A₄⁴=96种．
故选：B．

点评本题考查排列组合以及简单的计数原理的应用，正确分组是解题的关键，考查分析问题解决问题的能力．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

10．计算x+y+z=6的正整数解有多少组？

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

11．{a_n}的前n项和为S_n，且{$\frac{{S}_{n}}{n}$}为等差数列，S₁₉=171，则a₁₀为（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

8．如果sin（π+α）=-$\frac{\sqrt{3}}{2}$，那么cos（$\frac{π}{2}$+α）=（　　）

A．

$\frac{1}{2}$

B．

-$\frac{1}{2}$

C．

$\frac{\sqrt{3}}{2}$

D．

-$\frac{\sqrt{3}}{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

15．已知△ABC的内角A，B，C的对边分别为a，b，c，且b=acosc+$\frac{{\sqrt{3}}}{3}$csinA．
（Ⅰ）求角A的大小；
（Ⅱ）当a=3时，求△ABC周长的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

5．

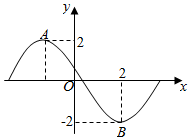函数f（x）=2sin（ωx+φ）（ω＞0，0≤φ≤π）的部分图象如图所示，其中A，B两点之间的距离为5，则f（x）的递减区间是（　　）

A．

[3k-1，3k+2]（k∈Z）

B．

[3k-4，3k-1]（k∈Z）

C．

[6k-1，6k+2]（k∈Z）

D．

[6k-4，6k-1]（k∈Z）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

12．

雾霾天气是一种大气污染状态，PM2.5被认为是造成雾霾天气的“元凶”，PM2.5日均值越小，空气质量越好．国家环境标准设定的PM2.5日均值（微克/立方米）与空气质量等级对应关系如表：

PM2.5日均值（微克/立方米）	0--35	35--75	75--115	115--150	150--250	250以上
空气质量等级	1级优	2级良	3级轻度污染	4级中度污染	5级重度污染	6级严重污染

由某市城市环境监测网获得4月份某5天甲、乙两城市的空气质量指数数据，用茎叶图表示，如图所示．
（Ⅰ）试根据统计数据，分别写出两城区的PM2.5日均值的中位数，并从中位数角度判断哪个城区的空气质量较好？
（Ⅱ）考虑用频率估计概率的方法，试根据统计数据，估计甲城区某一天空气质量等级为3级轻度污染的概率；
（Ⅲ）分别从甲、乙两个城区的统计数据中任取一个，试求这两城区空气质量等级相同的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

9．任何进制数均可转换为十进制数，如八进制（507413）₈转换成十进制数，是这样转换的：（507413）₈=5×8⁵+0×8⁴+7×8³+4×8²+1×8+3=167691，十六进制数（23456）₁₆是这样转换的：（23456）₁₆=2×16⁴+3×16³+4×16²+5×16+6=144470．那么将二进制数（1101）₂转换成十进制数，这个十进制数是（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

10．终边落在第二象限的角组成的集合为（　　）

	A．	{α\|kπ＜α＜$\frac{π}{2}$+kπ，k∈Z}		B．	{α\|$\frac{π}{2}$+kπ＜α＜π+kπ，k∈Z}
	C．	{α\|2kπ＜α＜$\frac{π}{2}$+2kπ，k∈Z}		D．	{α\|$\frac{π}{2}$+2kπ＜α＜π+2kπ，k∈Z}

查看答案和解析>>

同步练习册答案