
分析 利用函数满足的性质,分析4个命题,即可得出结论.
解答 解:①x=-2,可得f(2)=f(-2)+f(2),∴f(2)=0,正确;
②f(x+4)=-f(-x),∴f(x+4)+f(-x)=0,∴函数f(x)的图象关于点(2,0)成对称中心,正确;
③对任意的x1,x2∈[0,2],都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0成立,∴函数f(x)在(0,2)上单调递减,
∵函数f(x)的图象关于点(2,0)成对称中心,∴函数f(x)在(0,4)上单调递减,
∴函数f(x)在(-4,0)上单调递减,正确;
④函数f(x)在(-6,6)上有3个零点,即-4,-2,0,2,4,不正确.
故答案为:①②③.
点评 本题考查新定义,考查函数的性质,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x≤1} | B. | {x|-1≤x<1} | C. | {x|-1≤x≤1} | D. | {x|-1<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2] | B. | [0,2] | C. | [1,2] | D. | [-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b,c都大于0 | B. | a,b,c都是非负数 | ||
| C. | a,b,c至多两个负数 | D. | a,b,c至多一个负数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $8\sqrt{2}$ | B. | 46 | C. | $2\sqrt{23}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
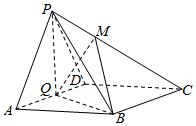 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com