
| A. | $8\sqrt{2}$ | B. | 46 | C. | $2\sqrt{23}$ | D. | 32 |
分析 画出图形,将$\overrightarrow{A{C}_{1}}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}_{1}}$,两边平方求值,然后开方求线段长度.
解答 解:如图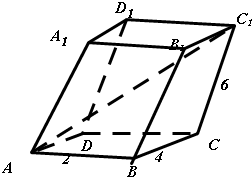 因为$\overrightarrow{A{C}_{1}}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}_{1}}$,
因为$\overrightarrow{A{C}_{1}}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}_{1}}$,
并且AB=2,AD=4,AA1=6,∠A1AB=∠A1AD=60°,
所以$|\overrightarrow{A{C}_{1}}{|}^{2}={\overrightarrow{AB}}^{2}+{\overrightarrow{A{D}^{\;}}}^{2}+{\overrightarrow{A{A}_{1}}}^{2}$$+2\overrightarrow{AB}•\overrightarrow{AD}+2\overrightarrow{AB}•\overrightarrow{A{A}_{1}}+2\overrightarrow{AD}•\overrightarrow{A{A}_{1}}$=4+16+36+0+2×2×6×$\frac{1}{2}$+2×4×$6×\frac{1}{2}$=92,
所以AC1=$\sqrt{92}=2\sqrt{23}$;
故选C.
点评 本题考查了利用平面向量求空间线段的长度;关键是所求向量化,利用向量表示.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [1,2] | C. | [1,$\frac{3}{2}$] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{22}{7}$ | B. | $\frac{63}{20}$ | C. | $\frac{78}{25}$ | D. | $\frac{109}{35}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
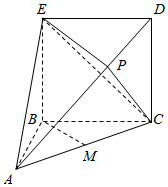 在几何体ABCDE中,矩形BCDE的边CD=2,BC=AB=1,∠ABC=90°,直线EB⊥平面ABC,P是线段AD上的点,且AP=2PD,M为线段AC的中点.
在几何体ABCDE中,矩形BCDE的边CD=2,BC=AB=1,∠ABC=90°,直线EB⊥平面ABC,P是线段AD上的点,且AP=2PD,M为线段AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{22}{7}$ | B. | $\frac{63}{20}$ | C. | $\frac{78}{25}$ | D. | $\frac{109}{35}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
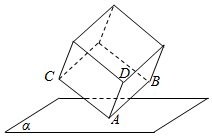 如图,棱长为3的正方体的顶点A在平面α上,三条棱AB,AC,AD都在平面α的同侧,若顶点B,C到平面α的距离分别为1,$\sqrt{2}$,则顶点D到平面α的距离是$\sqrt{6}$.
如图,棱长为3的正方体的顶点A在平面α上,三条棱AB,AC,AD都在平面α的同侧,若顶点B,C到平面α的距离分别为1,$\sqrt{2}$,则顶点D到平面α的距离是$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | a>c>b | D. | b>a>c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com