
| A. | $\frac{22}{7}$ | B. | $\frac{63}{20}$ | C. | $\frac{78}{25}$ | D. | $\frac{109}{35}$ |
分析 利用“调日法”进行计算,即可得出结论.
解答 解:第一次用“调日法”后得$\frac{16}{5}$是π的更为精确的过剩近似值,即$\frac{31}{10}$<π<$\frac{16}{5}$,
第二次用“调日法”后得$\frac{47}{15}$是π的更为精确的过剩近似值,即$\frac{47}{15}$<π<$\frac{16}{5}$;
第三次用“调日法”后得$\frac{63}{20}$是π的更为精确的过剩近似值,即$\frac{47}{15}$<π<$\frac{63}{20}$,
第四次用“调日法”后得$\frac{22}{7}$是π的更为精确的过剩近似值,即$\frac{47}{15}$<π<$\frac{22}{7}$,
故选:A.
点评 本题考查“调日法”,考查学生的计算能力,比较基础.


科目:高中数学 来源: 题型:解答题
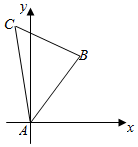 在平面直角坐标系中,两点P1(x1,y1),P2(x2,y2)间的“L-距离”定义为|P1P2|=|x1-x2|+|y1-y2|.现将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的斜率为k,0≤k≤$\sqrt{3}$.求:当|BC|取最大值时,边AB所在直线的斜率的值.
在平面直角坐标系中,两点P1(x1,y1),P2(x2,y2)间的“L-距离”定义为|P1P2|=|x1-x2|+|y1-y2|.现将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的斜率为k,0≤k≤$\sqrt{3}$.求:当|BC|取最大值时,边AB所在直线的斜率的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b,c都大于0 | B. | a,b,c都是非负数 | ||
| C. | a,b,c至多两个负数 | D. | a,b,c至多一个负数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $8\sqrt{2}$ | B. | 46 | C. | $2\sqrt{23}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
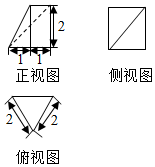 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四面体P-ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC=$\frac{2\sqrt{3}}{3}$.
如图,在四面体P-ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC=$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com