
| A. | $\frac{22}{7}$ | B. | $\frac{63}{20}$ | C. | $\frac{78}{25}$ | D. | $\frac{109}{35}$ |
分析 利用“调日法”进行计算,即可得出结论.
解答 解:由调日法运算方法可知,
第一次用“调日法”后得$\frac{16}{5}$是π的更为精确的过剩近似值,即$\frac{31}{10}<π<\frac{16}{5}$,
第二次用调日法后得$\frac{47}{15}$是π更为精确的不足近似值,即$\frac{47}{15}<π<\frac{16}{5}$,
第三次用调日法后得$\frac{63}{20}$是π更为精确的过剩近似值,即$\frac{47}{15}<π<\frac{63}{20}$,
故第三次调日法后得到$\frac{63}{20}$为π的近似分数.
故选B.
点评 本题考查“调日法”,考查学生的计算能力,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | {α|kπ<α<$\frac{π}{2}$+kπ,k∈Z} | B. | {α|$\frac{π}{2}$+kπ<α<π+kπ,k∈Z} | ||
| C. | {α|2kπ<α<$\frac{π}{2}$+2kπ,k∈Z} | D. | {α|$\frac{π}{2}$+2kπ<α<π+2kπ,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b,c都大于0 | B. | a,b,c都是非负数 | ||
| C. | a,b,c至多两个负数 | D. | a,b,c至多一个负数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $8\sqrt{2}$ | B. | 46 | C. | $2\sqrt{23}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
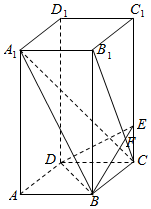 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
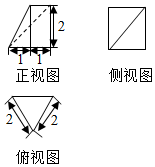 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
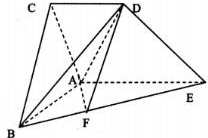 在如图所示的几何体中,△ABC为正三角形,AE和CD都垂直于平面ABC,且AE=AB=2,CD=1,F在线段BE上.
在如图所示的几何体中,△ABC为正三角形,AE和CD都垂直于平面ABC,且AE=AB=2,CD=1,F在线段BE上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com