
【题目】给出以下四个命题:
①设![]() 是空间中的三条直线,若
是空间中的三条直线,若![]() ,
,![]() ,则
,则![]() .
.
②在面积为![]() 的
的![]() 的边
的边![]() 上任取一点
上任取一点![]() ,则
,则![]() 的面积大于
的面积大于![]() 的概率为
的概率为![]() .
.
③已知一个回归直线方程为![]()
![]() ,则
,则![]() .
.
④数列![]() 为等差数列的充要条件是其通项公式为
为等差数列的充要条件是其通项公式为![]() 的一次函数.
的一次函数.
其中正确命题的充号为________.(把所有正确命题的序号都填上)
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】已知某企业近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:
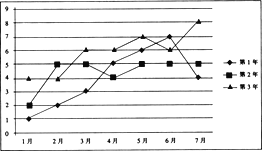
(1)试问这3年的前7个月中哪个月的月平均利润最高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
月份x | 1 | 2 | 3 | 4 |
利润y(单位:百万元) | 4 | 4 | 6 | 6 |
相关公式: 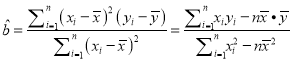 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,右顶点到左焦点的距离为
,右顶点到左焦点的距离为![]() ,
,![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的左、右两个焦点.
的左、右两个焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知椭圆![]() 的切线
的切线![]() (与椭圆
(与椭圆![]() 有唯一交点)的方程为
有唯一交点)的方程为![]() ,切线
,切线![]() 与直线
与直线![]() 和直线
和直线![]() 分别交于点
分别交于点![]() 、
、![]() ,求证:
,求证:![]() 为定值,并求此定值;
为定值,并求此定值;
(3)设矩形![]() 的四条边所在直线都和椭圆
的四条边所在直线都和椭圆![]() 相切(即每条边所在直线与椭圆
相切(即每条边所在直线与椭圆![]() 有唯一交点),求矩形
有唯一交点),求矩形![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且过点
,且过点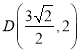 .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,与椭圆
两点,与椭圆![]() 相交于
相交于![]() 两点,
两点,![]() (
(![]() 为坐标原点),
为坐标原点),![]() 为抛物线的焦点,求
为抛物线的焦点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·衢州调研)已知四棱锥P-ABCD的底面ABCD是菱形,∠ADC=120°,AD的中点M是顶点P在底面ABCD的射影,N是PC的中点.

(1)求证:平面MPB⊥平面PBC;
(2)若MP=MC,求直线BN与平面PMC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数据的收集和整理在当今社会起到了举足轻重的作用,它用统计的方法来帮助人们分析以往的行为习惯,进而指导人们接下来的行动.
某支足球队的主教练打算从预备球员甲、乙两人中选一人为正式球员,他收集到了甲、乙两名球员近期5场比赛的传球成功次数,如下表:
场次 | 第一场 | 第二场 | 第三场 | 第四场 | 第五场 |
甲 | 28 | 33 | 36 | 38 | 45 |
乙 | 39 | 31 | 43 | 39 | 33 |
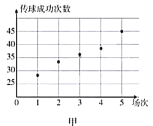
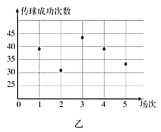
(1)根据这两名球员近期5场比赛的传球成功次数,完成茎叶图(茎表示十位,叶表示个位);分别在平面直角坐标系中画出两名球员的传球成功次数的散点图;
(2)求出甲、乙两名球员近期5场比赛的传球成功次数的平均值和方差;
(3)主教练根据球员每场比赛的传球成功次数分析出球员在场上的积极程度和技术水平,同时根据多场比赛的数据也可以分析出球员的状态和潜力.你认为主教练应选哪位球员?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() 是等腰直角三角形,
是等腰直角三角形,![]() .
.
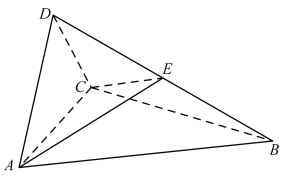
(I)证明:平面![]() 平面ABC;
平面ABC;
(II)点E在BD上,若平面ACE把三棱锥![]() 分成体积相等的两部分,求二面角
分成体积相等的两部分,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)设函数![]() ,试判断函数
,试判断函数![]() 是否存在最小值,若存在,求出最小值,若不存在,请说明理由.
是否存在最小值,若存在,求出最小值,若不存在,请说明理由.
(Ⅲ)当![]() 时,写出
时,写出![]() 与
与![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为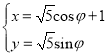 (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(1)求C1的极坐标方程;
(2)若C1与曲线C2:ρ=2sinθ交于A,B两点,求|OA||OB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com