
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在实数
,若存在实数![]() 及
及![]() 、
、![]() (
(![]() )使得对于任意
)使得对于任意![]() 都有
都有![]() 成立,则称函数
成立,则称函数![]() 是带状函数;若
是带状函数;若![]() 存在最小值
存在最小值![]() ,则称
,则称![]() 为带宽.
为带宽.
(1)判断函数![]() 是不是带状函数?如果是,指出带宽(不用证明);如果不是,请说明理由;
是不是带状函数?如果是,指出带宽(不用证明);如果不是,请说明理由;
(2)求证:函数![]() (
(![]() )是带状函数;
)是带状函数;
(3)求证:函数![]() 是带状函数的充要条件是
是带状函数的充要条件是![]() .
.
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,若
时,若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若定义在![]() 上奇函数
上奇函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时,![]() ,求
,求![]() 在
在![]() 上的解析式;
上的解析式;
(3)对于(2)中的![]() ,若关于
,若关于![]() 的不等式
的不等式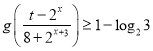 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在如图所示的6个点A、B、C、A1、、B1、C1上各装一个灯泡,要求同一条线段两端的灯泡不同色,则每种颜色的灯泡都至少用一个的安装方法共有 种(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着城市地铁建设的持续推进,市民的出行也越来越便利,根据大数据统计,某条地铁线路运行时,发车时间间隔![]() (单位:分钟)满足:
(单位:分钟)满足: ![]() ,平均每班地铁的载客人数
,平均每班地铁的载客人数![]() (单位:人)与发车时间间隔
(单位:人)与发车时间间隔![]() 近似地满足函数关系:
近似地满足函数关系: ,
,
(1)若平均每班地铁的载客人数不超过1560人,试求发车时间间隔![]() 的取值范围;
的取值范围;
(2)若平均每班地铁每分钟的净收益为![]() (单位:元),则当发车时间间隔
(单位:元),则当发车时间间隔![]() 为多少时,平均每班地铁每分钟的净收益最大?并求出最大净收益.
为多少时,平均每班地铁每分钟的净收益最大?并求出最大净收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 为两条不同的直线,
为两条不同的直线, ![]() ,
, ![]() 为两个不同的平面,对于下列四个命题:
为两个不同的平面,对于下列四个命题:
①![]() ,
, ![]() ,
, ![]() ,
, ![]() ②
②![]() ,
, ![]()
③![]() ,
, ![]() ,
, ![]() ④
④![]() ,
, ![]()
其中正确命题的个数有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高一学生有1000名学生参加一次数学小测验,随机抽取200名学生的测验成绩得如图所示的频率分布直方图:

(1)求该学校高一学生随机抽取的200名学生的数学平均成绩![]() 和标准差
和标准差![]() (同一组中的数据用该组区间的中点值做代表);
(同一组中的数据用该组区间的中点值做代表);
(2)试估计该校高一学生在这一次的数学测验成绩在区间![]() 之内的概率是多少?测验成绩在区间
之内的概率是多少?测验成绩在区间![]() 之外有多少位学生?(参考数据:
之外有多少位学生?(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】榆林市政府坚持保护环境和节约资源,坚持推进生态文明建设。若市财政局下拨专款100百万元,分别用于植绿护绿和处理污染两个生态维护项目,植绿护绿项目五年内带来的生态收益可表示为投放资金![]() (单位:百万元)的函数
(单位:百万元)的函数![]() (单位:百万元):
(单位:百万元):![]() ,处理污染项目五年内带来的生态收益可表示为投放资金
,处理污染项目五年内带来的生态收益可表示为投放资金![]() 单位:(单位:百万元)的函数
单位:(单位:百万元)的函数![]() (单位:百万元):
(单位:百万元):![]() 。
。
(1)设分配给植绿护绿项目的资金为![]() (百万元),则两个生态项目五年内带来的收益总和为y,写出y关于
(百万元),则两个生态项目五年内带来的收益总和为y,写出y关于![]() 的函数解析式和定义域;
的函数解析式和定义域;
(2)试求出y的最大值,并求出此时对两个生态项目的投资分别为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com