
| n |
| |x|+m |
| n |
| |x|+m |
| 1 |
| |x|-1 |
|
| n |
| |x|+m |
| 1 |
| |x|-1 |
|
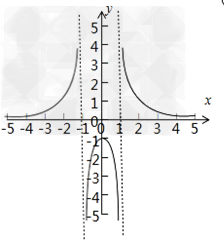 对于③,由图可知,函数f(x)在(-1,1)上不单调,故③错误;
对于③,由图可知,函数f(x)在(-1,1)上不单调,故③错误;| 1 |
| x+1 |
| 1 |
| x+1 |
| 1 |
| (x+1)2 |
| 1 |
| (x0+1)2 |
| 1 |
| x0+1 |
| 1 |
| |x|-1 |
| 1 |
| x+1 |
| 1 |
| x+1 |
| 1 |
| x+1 |
| 1 |
| x-1 |
| 1 |
| |x|-1 |


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:

| 1 |
| 10 |
| 1 |
| 6 |
| 综合得分k的范围 | 产品等级 | 产品利润率 |
| K≥85 | 一级品 | a |
| 75≤k<85 | 二级品 | 5a2 |
| 70≤k<75 | 三级品 | a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| a |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知椭圆C:
如图,已知椭圆C:| y2 |
| a2 |
| x2 |
| b2 |
| 1 |
| 2 |
| QM |
| QN |
查看答案和解析>>
科目:高中数学 来源: 题型:
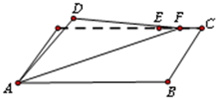 如图,在长方形ABCD中,AB=4,BC,E为DC的四等分点(靠近C处),F为线段EC上一动点(包括端点),现将△AFD沿AF折起,使D点在平面内的射影恰好落在边AB上,则当F运动时,二面角D-AF-B的平面角余弦值的变化范围为
如图,在长方形ABCD中,AB=4,BC,E为DC的四等分点(靠近C处),F为线段EC上一动点(包括端点),现将△AFD沿AF折起,使D点在平面内的射影恰好落在边AB上,则当F运动时,二面角D-AF-B的平面角余弦值的变化范围为查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com